正态分布,英文名 normal distribution,意为“正常的分布”,台湾省将其译为“常态分布”。它是如此之“正常”,以致于渗透到我们生活的方方面面。上至九天星河的光度分布,下至气体分子的运动速率,无不服从正态分布。它可以说,是世界背后的抓手之一。为此,我们来进一步了解正态分布。
话说数学王子高斯在写作《天体运动论》时发现手头上的观测数据存在误差。他想知道误差服从什么样的分布函数,为此展开了下列推导。
设误差分布的概率密度函数为 f (x), 高斯手中的观测数据分别为
真实值为
则出现眼前情况的概率为
(ps:1、由于眼前已经出现了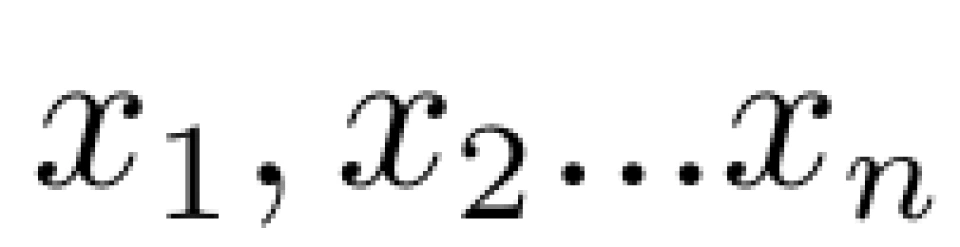 这种情况,所以我们认为这种情况出现的概率最大。所以,在之后的数学处理中,我们将千方百计地使得 p 取更大的值。
这种情况,所以我们认为这种情况出现的概率最大。所以,在之后的数学处理中,我们将千方百计地使得 p 取更大的值。
2、高斯认为,偶然误差可以通过多次测量求平均值来抵消,即
我们由生活经验可知其正确性及可靠性。)
对于函数
所以,
令
则有
令 i = 2, 得:
即 g (x) 为奇函数
同理,令i=3,得:
若令
结合g(x)为奇函数的推论,可得
所以,g (x)满足柯西方程,易得,
即
由概率密度函数的性质可知,
所以,c < 0,
即
(为了使思维连贯,这里直接运用了高斯积分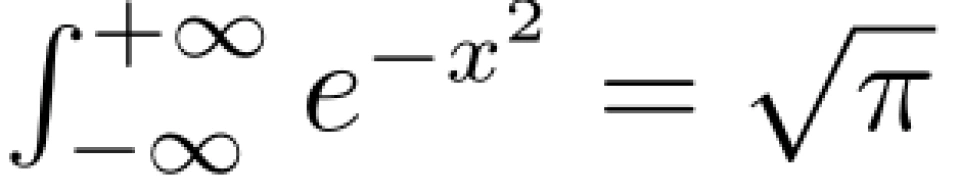 的结论,的结论,其详细推导则放在文末)
的结论,的结论,其详细推导则放在文末)
由此可得,
即
回到函数 ln(L(x)) 中,则有
我们要千方百计地使其取到最大值,而就目前的信息来看,只知道 c < 0, 所
令其为零,可得
(其中 σ 指标准差)则 f (x) 可改写为
(请注意,这里的自标量 x 指的是随机误差) 若以 µ 代表观测数据的真实值(平均值)x 0 , 并以 x − µ 替换 x, 那么替换后的自变量 x 即为观测值。到这
里,就得到了课本中的正态分布表达式
终于推出了正态分布的表达式,接下来简单地介绍正态分布的一些性质。
1、正态分布式“正常”的分布,它渗透于我们生产生活的方方面面。工人的生产效率,学生的考试成绩,全国各市的汽车价格分布等等等等,在样
本容量足够大,代表性足够强时都服从正态分布。基于此,我们可以很方便地估计手头的数据在整体中的地位。比如,某软件测得部分电脑的开机时间,就可以据此建立正态分布的模型,并根据用户的开机时长估计它能战胜全国百分之多少的用户。
2、正态分布的平均值即为其数学期望。我们知道,数学期望代表的是事件的长期价值,而在正态分布中,平均值即为数学期望。为此,我们经常用平均值,而非极端值衡量整体在某一方面水平的高低。如用平均分衡量学校的教学能力,用平均薪金刻画单位的工薪水平等。当脱离了正态分布的背景后,平均值将失去刻画整体水平高低的能力。例如,比尔·盖茨与九个乞丐组成的集团人均资产超过百亿,这种资产分布显然不符合正态分布,平均值也失去了其衡量整体资产的意义。
3、在正态分布中,大部分随机变量都集中在平均值 µ 附近,极端数据占比极小
。这就使正态分布具有很强的稳定性,即抵抗极端数据影响的能力。就比如说,广东省一车主购入一辆劳斯莱斯银魅(15.5 亿),也不会对全省汽车价格的平均值造成很剧烈的影响。
最后,高斯积分大放送。对于积分
我们有
由于 x,y 是在各自的积分空间中积分,没有相互影响,因此上式可作如下变形
将直角坐标转换到极坐标,则有
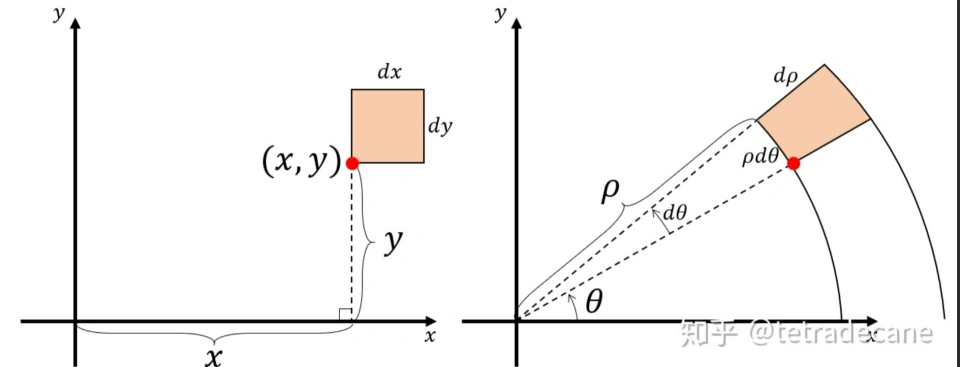
并且,(dx)*(dy) 在直角坐标系中可以指任意该坐标平面中的任意一块面积微元,而在极坐标中,任意一块面积微元的表示方法为 r ∗ dρ ∗ dθ 如下图所示
接下来是积分上下限的问题,在直角坐标中,x 和 y 的积分上下限分别都是正无穷和负无穷,并对于任意 x 和 y, 都只积了一遍,也就是把整个
坐标平面扫了一遍。在极坐标中,为了达到同样的效果,则必须 r 的积分上下限分别是正无穷和 0,θ 的积分上下限分别是 2π 和 0。
因此,我们有
接下来是运算,
所以,
高斯积分放送完毕!!!!!!!!!!!!!
参考资料:
1、MATHSING 正态分布的推导
参考资料:
1、MATHSING 正态分布的推导 _哔哩哔哩_bilibili
2、回到 2049 【2049 日报】S05E352 正态分布_哔哩哔哩_bilibili
3、蓝德岗的猫 【高斯积分】积分 e ( −x 2 ) 从负无穷到正无穷_哔哩哔哩_bilibili
呼,终于写完了,敲这种东西可不轻松呀 ![[s-4]](https://www.bokeyuan.net/pic/image/emoji/cas/4.png)



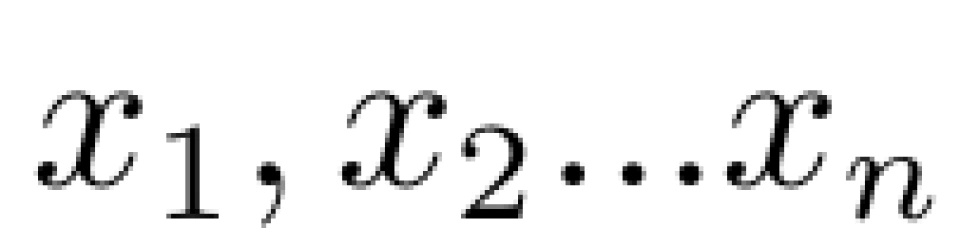
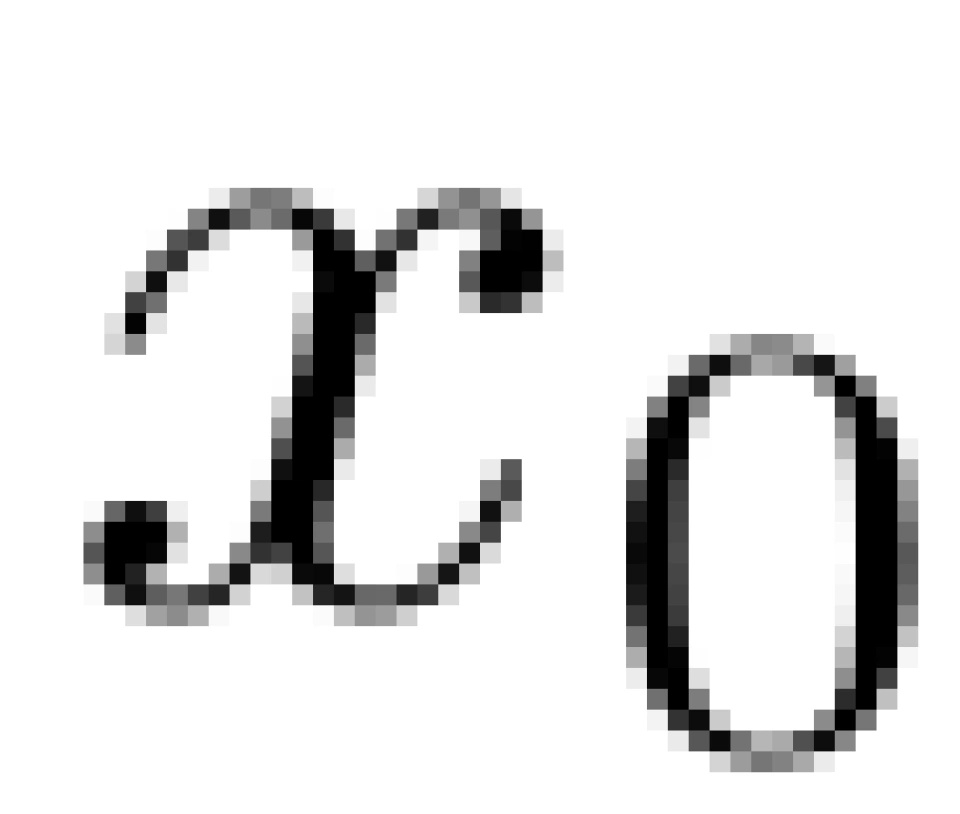
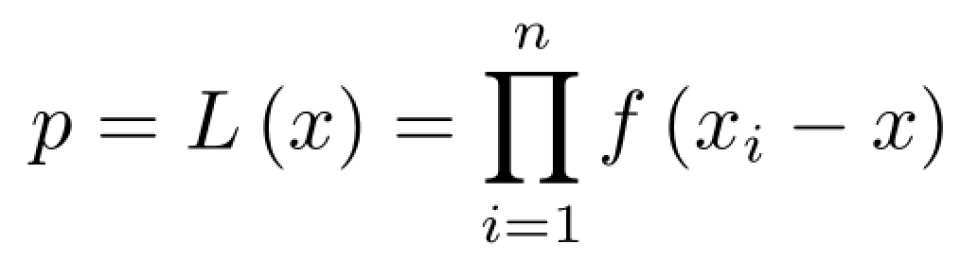
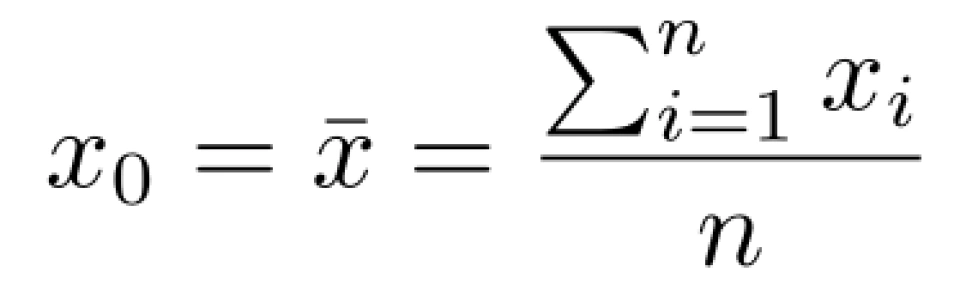
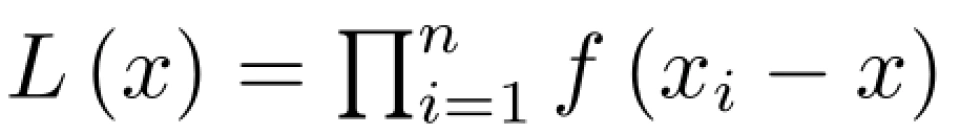
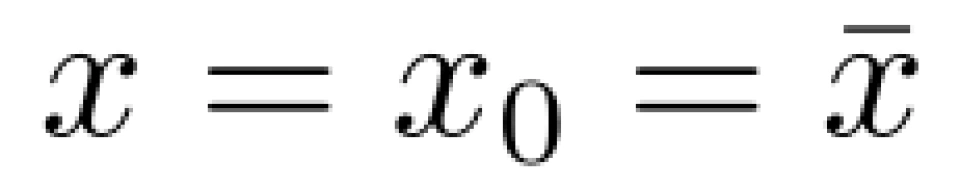
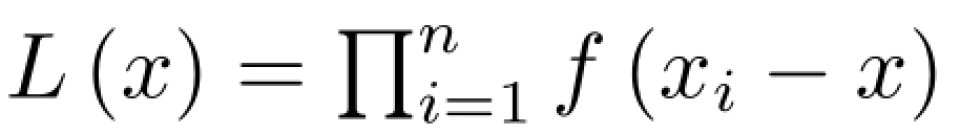
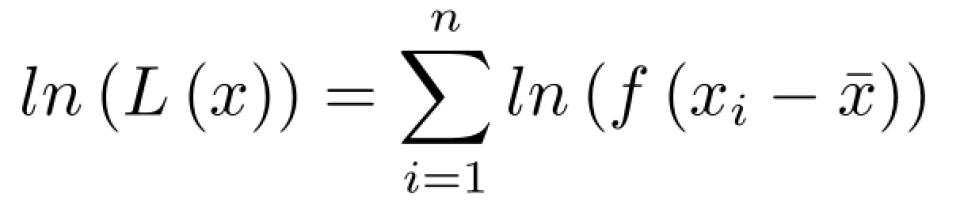
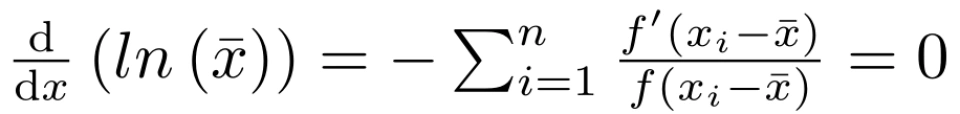
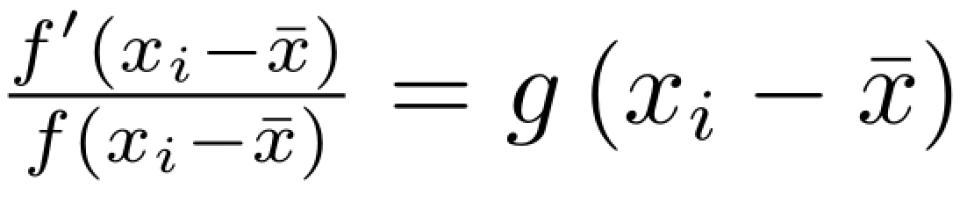
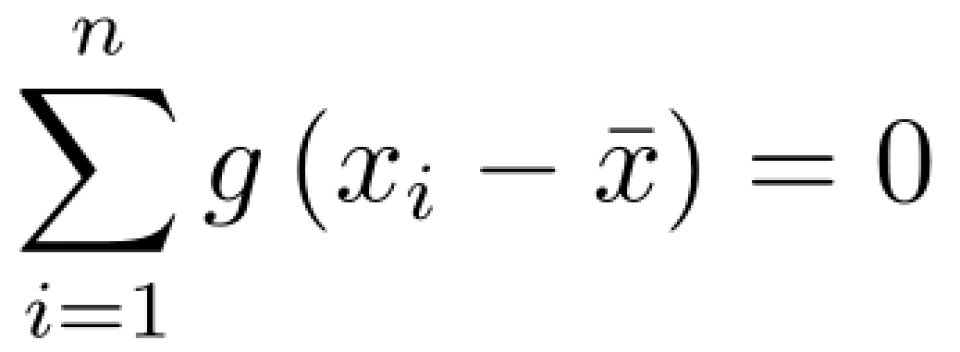
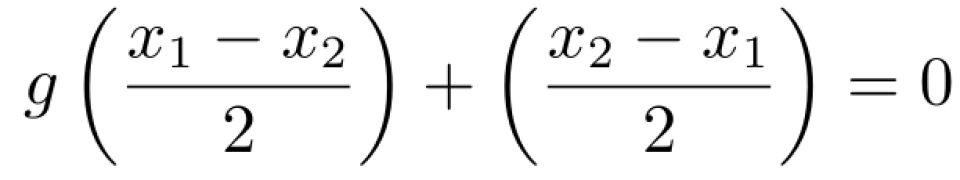
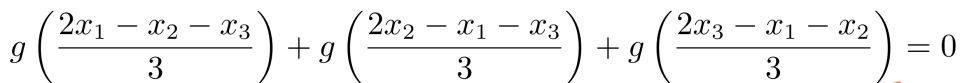
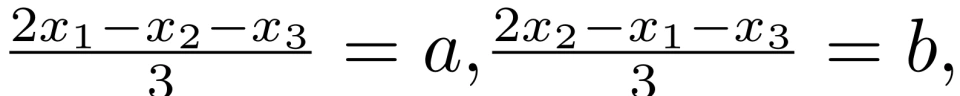
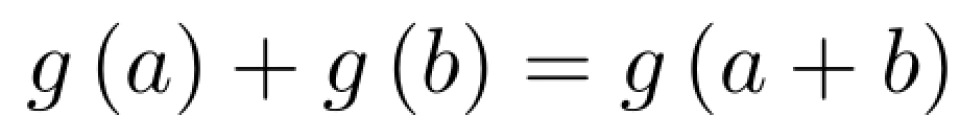
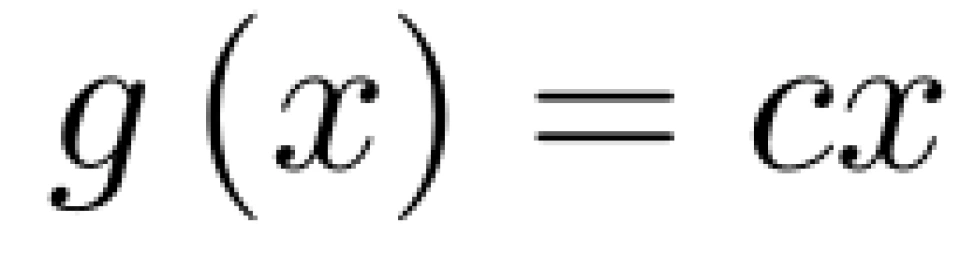
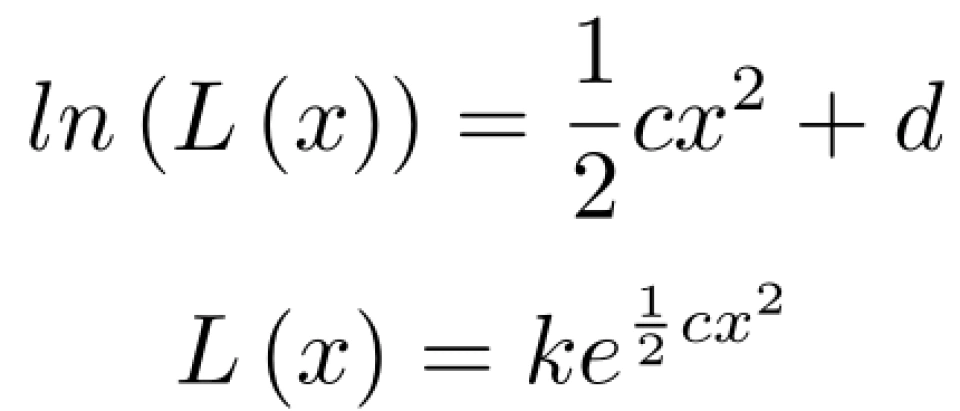
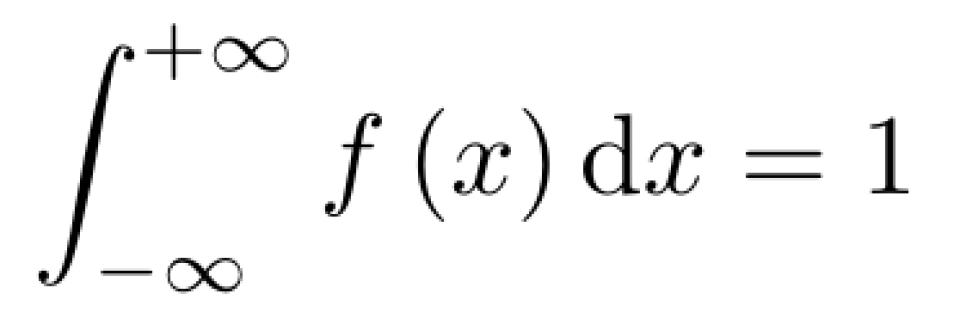
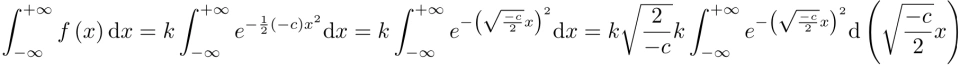
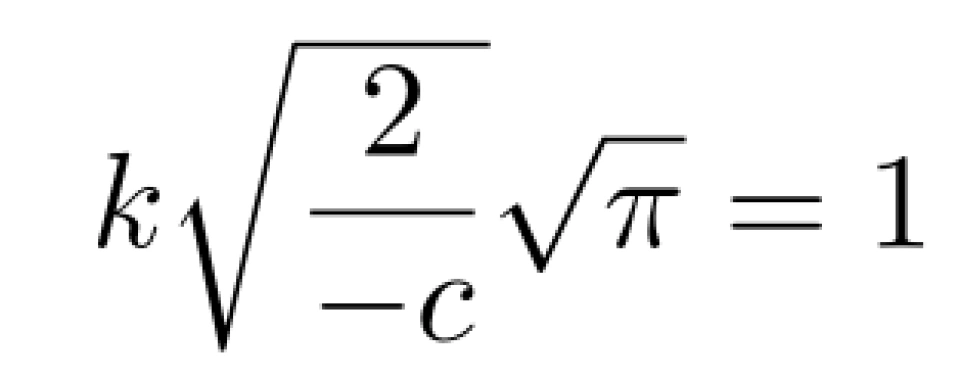
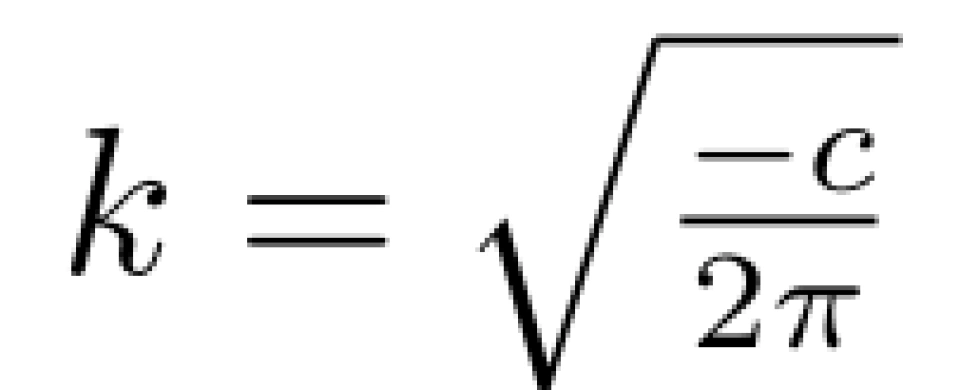
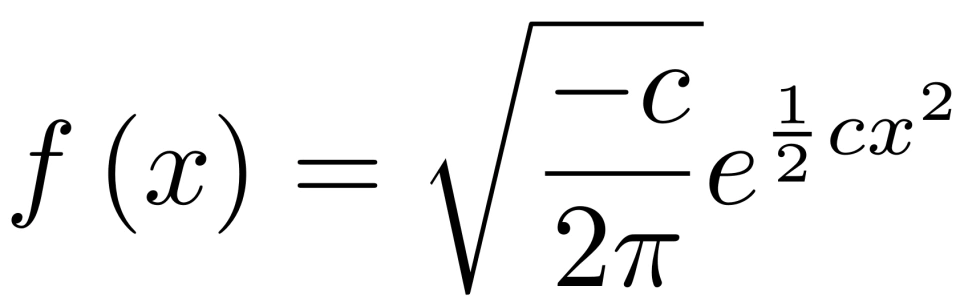
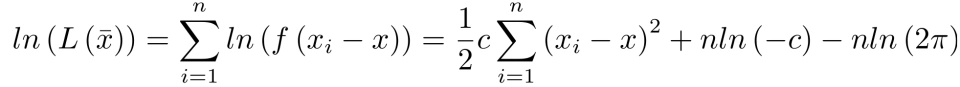
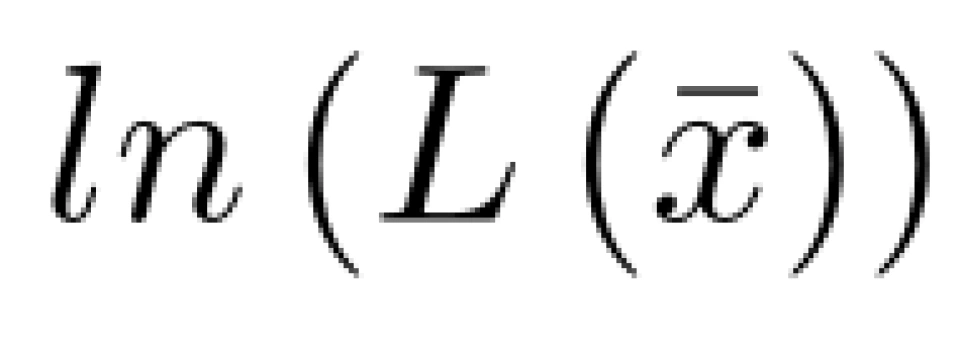
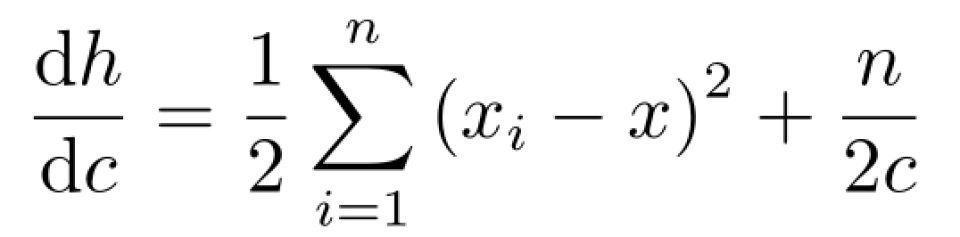
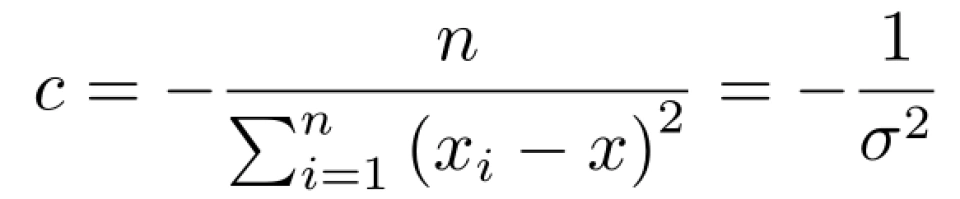
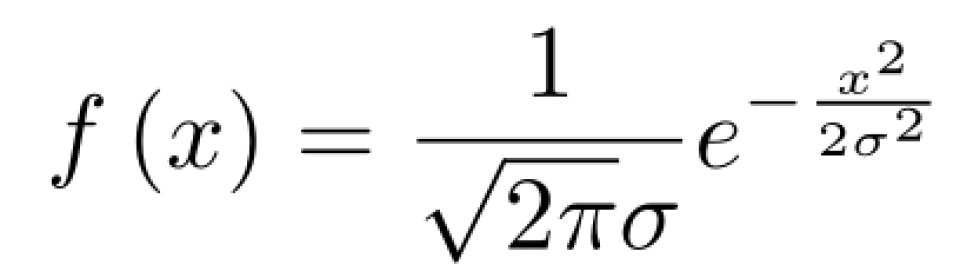
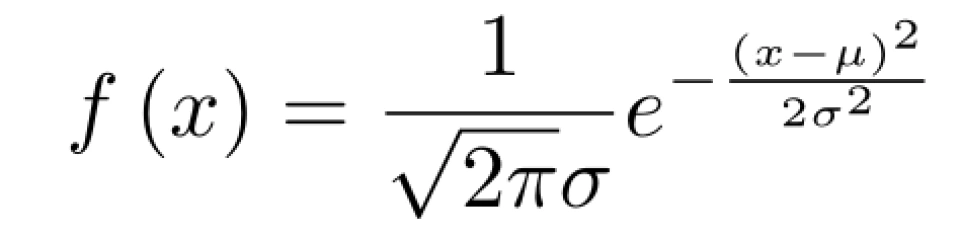
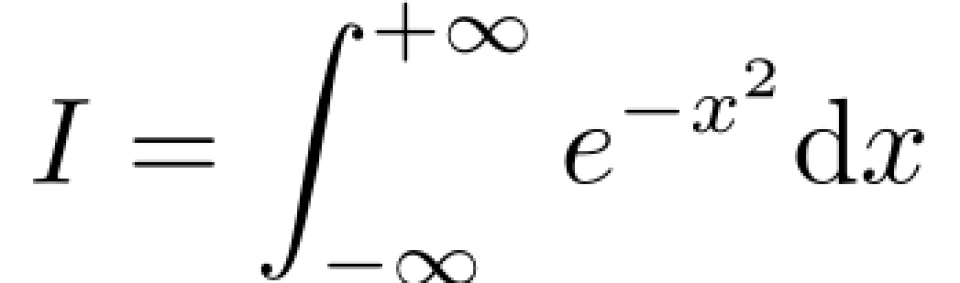
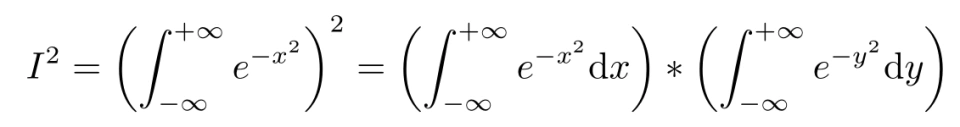
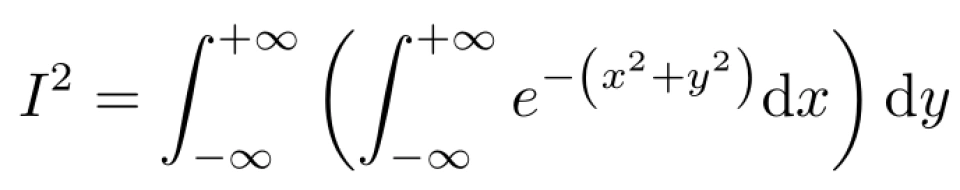
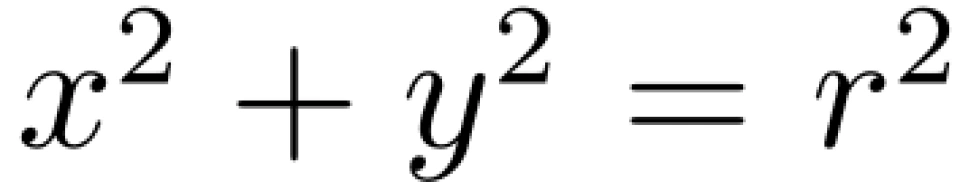
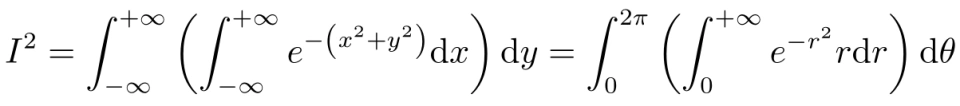
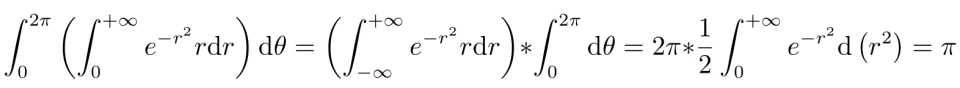















如果文章有什么问题,欢迎在评论区指出。如果对文章内容有什么疑惑,也欢迎在评论区提出,来一起交流学习。![[s-14]](https://www.bokeyuan.net/pic/image/emoji/cas/14.png)
![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)