import matplotlib.pyplot as plt import numpy as np from scipy import constants as const from scipy import sparse # 稀疏矩阵 from scipy.sparse.linalg import eigs # 稀疏线性代数。矩阵 #这部分给出常数 hbar =const.hbar e =const.e m_e =const.m_e pi =const.pi epsilon_0=const.epsilon_0 joul_to_eV=e #定义r的函数 def calculate_potential_term(r): potential=e**2/(4.0*pi*epsilon_0)/r sparse.diags((potential)) return potential def calculate_angular_term(r): angular =l*(l+1)/r**2 angular_term=sparse.diags((angular)) return angular_term def calculate_laplace_three_point(r): h=r[1]-r[0] main_diag = -2.0 / h ** 2 * np.ones(N) off_diag = 1.0 / h ** 2 * np.ones(N - 1) laplace_term = sparse.diags([main_diag, off_diag, off_diag], (0, -1, 1)) return laplace_term def build_hamiltonian(r): laplace_term = calculate_laplace_three_point(r) angular_term = calculate_angular_term(r) potential_term = calculate_potential_term(r) hamiltonian = -hbar ** 2 / (2.0 * m_e) * (laplace_term - angular_term)-potential_term return hamiltonian def plot(r, densities, eigenvalues): plt.xlabel('x ($\\mathrm{\AA}$)') plt.ylabel('probability density ($\\mathrm{\AA}^{-1}$)') energies = ['E = {: >5.2f} eV'.format(eigenvalues[i].real / e) for i in range(3)] plt.plot(r * 1e+10, densities[0], color='blue', label=energies[0]) plt.plot(r * 1e+10, densities[1], color='green', label=energies[1]) plt.plot(r * 1e+10, densities[2], color='red', label=energies[2]) plt.legend() plt.show() return """ set up horizontal axis and hamiltonian """ N = 2000 l = 0 r = np.linspace(2e-9, 0.0, N, endpoint=False)#? hamiltonian = build_hamiltonian(r) """ solve eigenproblem """ number_of_eigenvalues = 30 eigenvalues, eigenvectors = eigs(hamiltonian, k=number_of_eigenvalues, which='SM')#? """ sort eigenvalue and eigenvectors """ eigenvectors = np.array([x for _, x in sorted(zip(eigenvalues, eigenvectors.T), key=lambda pair: pair[0])]) #zip() 函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。 #如果各个迭代器的元素个数不一致,则返回列表长度与最短的对象相同,利用 * 号操作符,可以将元组解压为列表。 eigenvalues = np.sort(eigenvalues) """ compute probability density for each eigenvector """ densities = [np.absolute(eigenvectors[i, :]) ** 2 for i in range(len(eigenvalues))] #len()字符串长度 #对数组中的每一个元素求其绝对值。np.abs是这个函数的简写。 """ plot results """ plot(r, densities, eigenvalues)
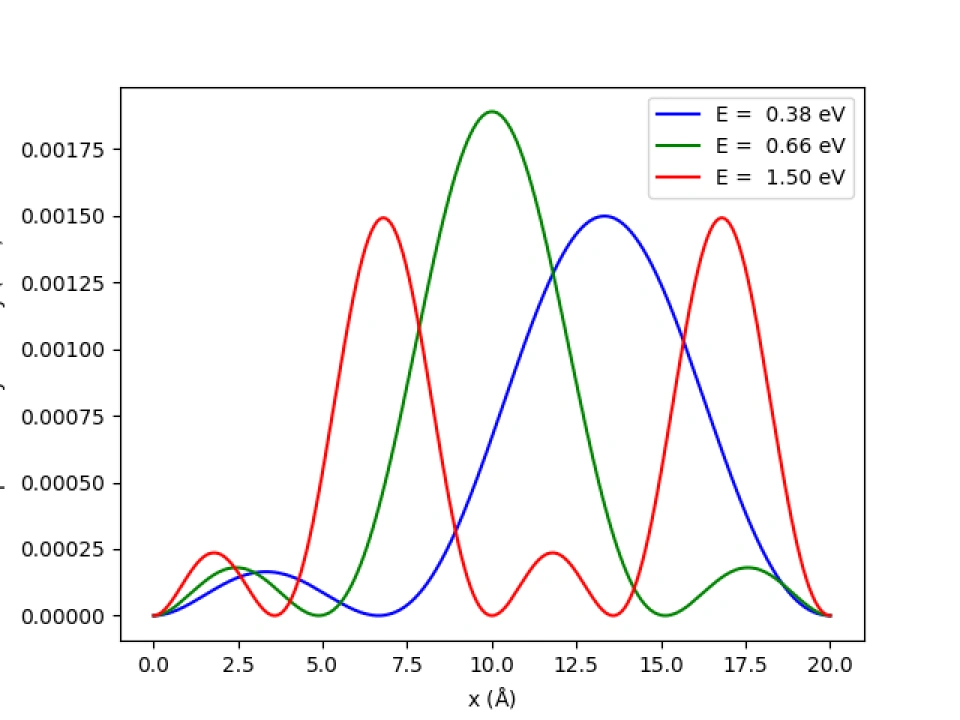
python代码:氢原子定态薛定谔方程,输出概率密度和本征值
⌬
Lv.14质子中子电子
🌼春暖花开
置顶
回复
闪电侠
Lv.3弦理论长度
普朗克
点个赞
回复
博科园小秘书
Lv.30恐龙
靓号:12345
11周年🎂
回复
博科园小秘书
Lv.30恐龙
靓号:12345
11周年🎂
要是有代码运行效果图就更好了 ![[s-57]](https://www.bokeyuan.net/pic/image/emoji/cas/57.png)
![[s-57]](https://www.bokeyuan.net/pic/image/emoji/cas/57.png)
回复
SMiu_PRC
Lv.9高能中微子
开普勒
点个赞
回复
幽魂西里
Lv.40心宿二
门捷列夫
你端坐在那里,我才知道我有多么浅薄,我曾忘情于两汉的歌赋,我曾惊讶于唐宋诗词,也曾流连于宋元的曲牌,如今而你才是人世间真正的圣人。
回复
仰望星空的猎豹
Lv.37卡普坦星
11周年🎂
厉害诶 ![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
回复
水仙
Lv.1量子泡沫
什么软件?
回复
请登录之后再进行评论
登录















