科普驿站 第三十期
主题:你想知道的平行宇宙(下)
难度:B2
作者:咕咕黎、重蝶子、弦轴子
讲师:弦轴子
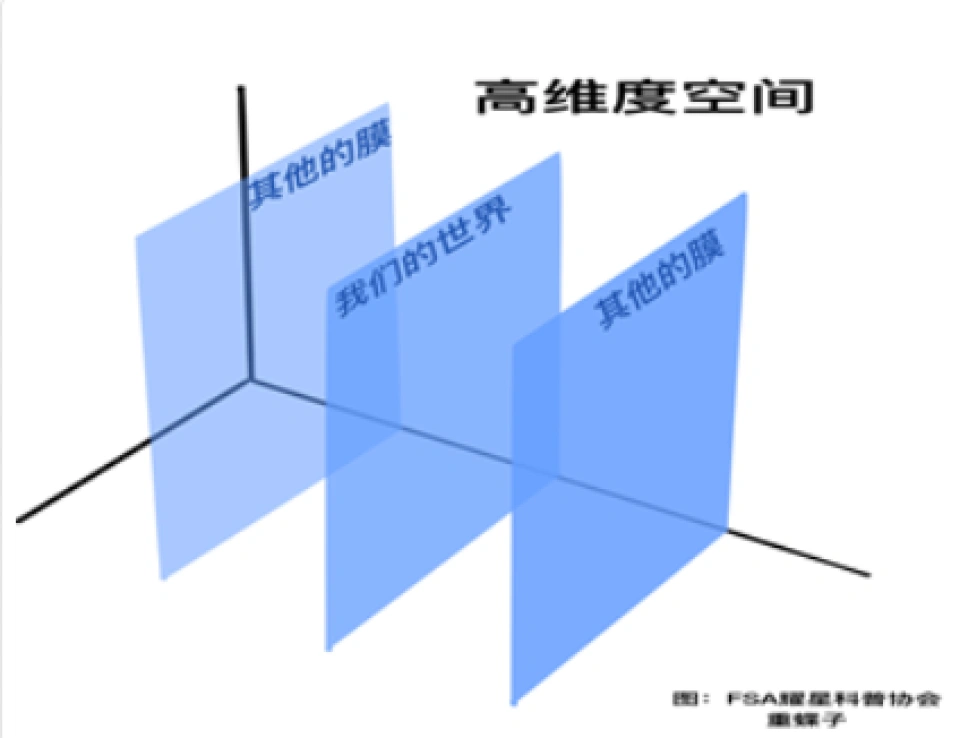
还有一种平行宇宙模型就是基于膜宇宙模型,这些理论假设我们在一个更高维度的空间中,不同模型这个高维度维度数目是不一样的,我们所生活的是三维的膜上,还有很多个我们平行或者交叉的膜,膜和膜之间只能通过引力相互作用,因为只有引力子才可以逃离出来。
膜之间的交叉碰撞就是黑洞,不同膜因为引力碰撞在一起也可以产生大爆炸现象,有些理论模型就认为我们的宇宙大爆炸有可能产生于两个膜之间的碰撞。
在高维空间中,不仅有我们生活的三维膜,还有很多跟我们平行的膜,他们也是独立的宇宙。这就是膜宇宙的多重宇宙理论。
下面我来简单介绍一下这类理论。不过在此之前我们先介绍一下额外维度在物理上是怎么引入的。
额外维理论:
通常,额外维理论中时空的维度是4+d形式的,这个d就是被引入的额外维度。不过值得注意的是,除了一些其他的额外维度理论,大部分额外维度理论引入的额外维度,并不是说是M^(4+d)模式,而是M^4xK^d,也就是我们的四维时空和一个d维空间的直积形式。不过,我们在现实生活中并没有发现这种额外维度存在的证据,因此最开始的引入模式中这些额维度是非常小的,被蜷缩在非常小的尺寸中,这个现象就称之为额维度的紧致化。
那么什么叫高维紧致化呢?
顾名思义,就是额外维度被紧致化在蜷缩维中,而紧致化意思是这些维度被紧化在一个流形上(流形:局域上同胚或者也就是等价于欧式空间的一种空间)。
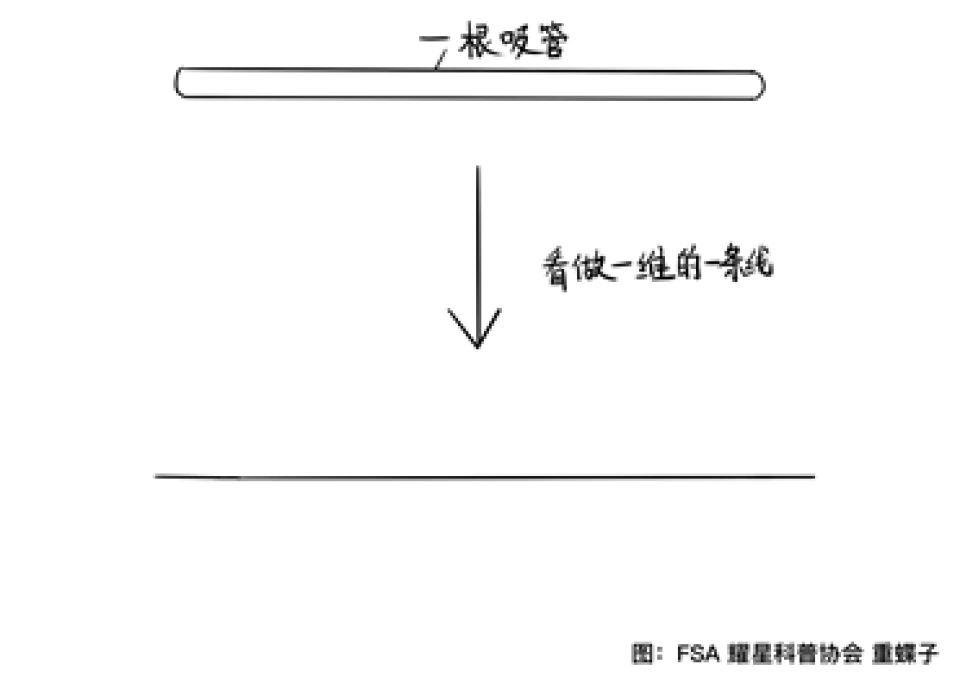
举个例子比如吸管:
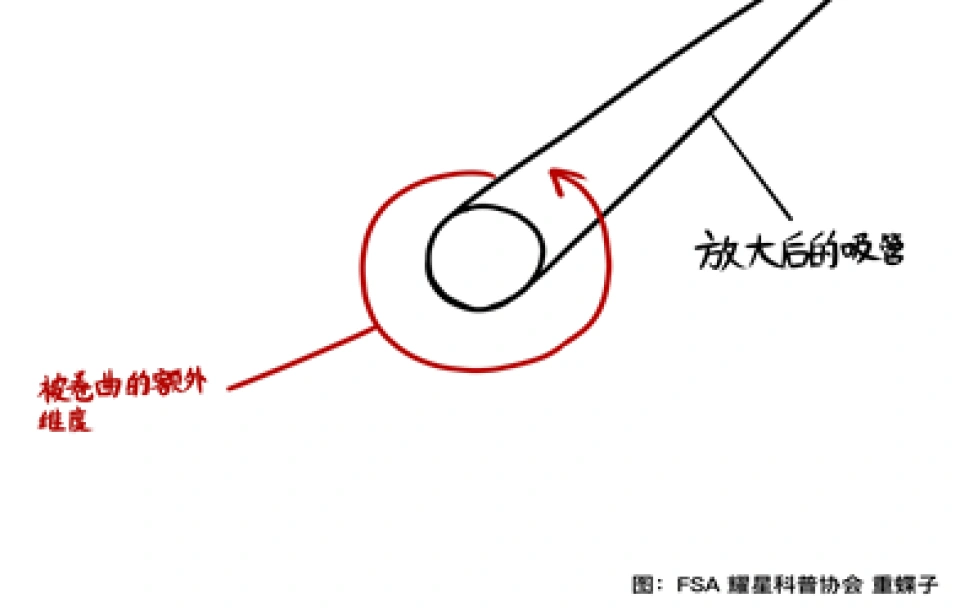
从远处看,吸管就是一维的线,但是当我们靠得非常近看的时候,会发现吸管表面的二维表面。
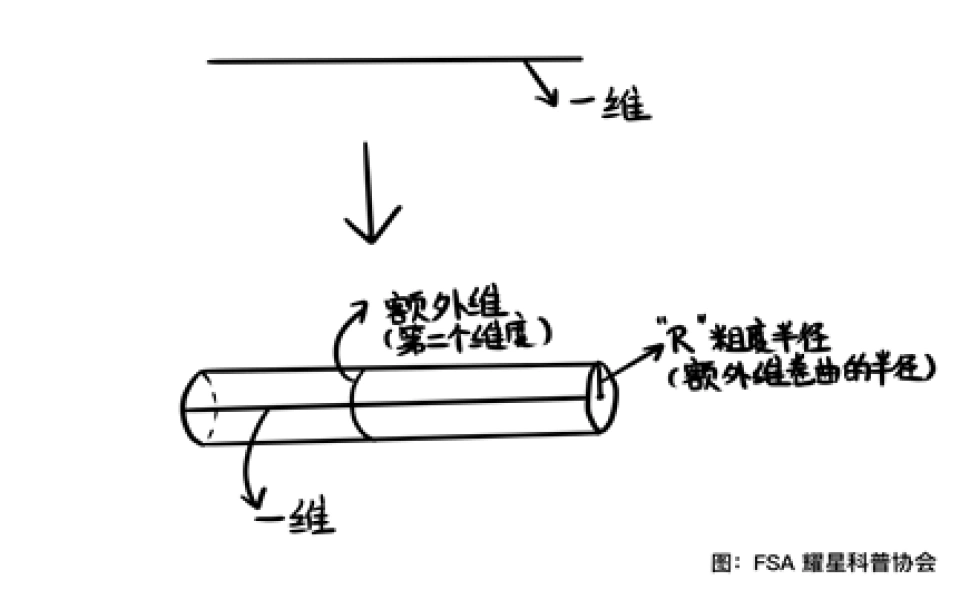
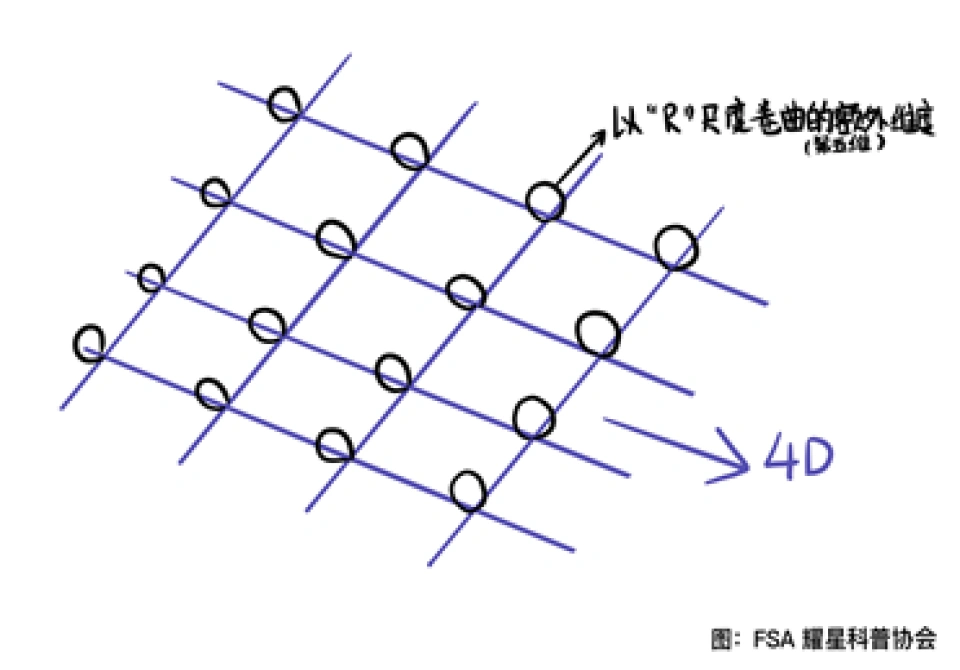
在这里二维的圆柱表面这个多出来的维度就沿着圆柱以吸管的粗度半径缠绕或者蜷缩。这个过程就是紧致化。
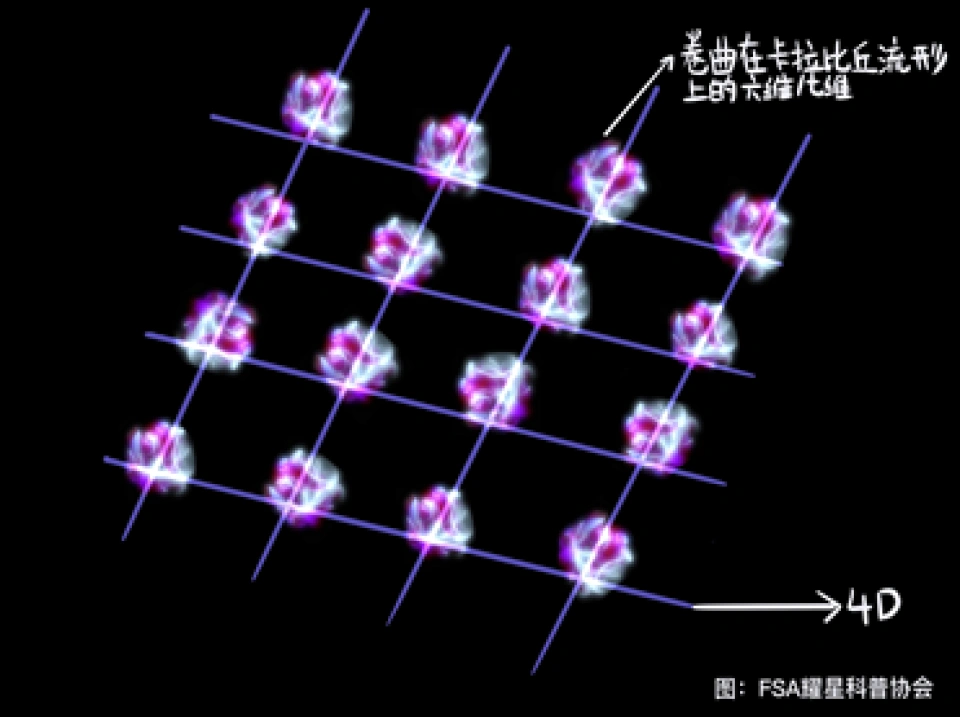
在弦理论中,剩下的六个维度蜷缩在六维的卡拉比丘流形上。而它们的特征尺度也就是粗度半径大概是一个普朗克尺度。
不过这种思想最早不是弦理论中提出的,而是1919年克鲁扎和克莱因提出来的,提出这种思想的目的就是为了统一当时已知两种相互作用,引力相互作用和电磁相互作用,因此它也被称为克鲁扎-克莱因理论(简称“KK理论”)。
尽管当时爱因斯坦在这方向上已经走很久了,但是他们俩用的是另一个思想。
最初的想法也很简单,既然引力是四维时空的弯曲,那么电磁力就是更高维度的时空弯曲。在数学上,他们可以很容易地写出五维时空的时空线元(也就是五维时空的两点之间距离函数/公式模板)与五维时空的时空度规。
相应的也可以得到五维时空上,类似于广义相对论引力场方程的一种场方程,即五维时空的爱因斯坦场方程。
但是,我们现实生活中确实没有这第五个维度,而且空间维度只有三个,因为我们现实中的电磁力和引力满足平方反比公式,或者高斯定理。任何形式的能量传播或者一些物理量的流动均满足高斯定理也就是球面关系。(注意到这一点,这个后来也成为检验一些额外维度存在的重要实验)
所以,如果这第五个维度存在,那么现实中将很难被探测到。他们设想这个第五维度非常小,被蜷缩在一个非常小的尺度上,并且是闭合的,也就是一定尺度的圆周。
近处看大概就是,一个四维时空,沿着第五维度的方向上每一个时空点都有一个一定尺度的圆周。
他们当时认为这种蜷缩的圆周尺度大概是一个普朗克尺度。
所以他们认为这第五维度必须看成是蜷缩的微小的圈,而且非常小。以至于我们在大尺度上很难感受到。所以,我们从大尺度上来看,我们的时空依然是四维的。
因此,当他们用这种紧致化的思想去处理他们的理论的时候,就会惊奇地发现五维的爱因斯坦场方程在四维时空会得到两种方程,第一种就是爱因斯坦引力场方程,第二种就是麦克斯韦电磁场方程。
也就是说,紧致化掉第5维之后得到的理论自动包括4维引力和麦克斯韦方程。
所以在当时这种思想理论看似解决了爱因斯坦的问题。当他们把这篇文章寄给爱因斯坦看的时候,爱因斯坦大为称赞,并声称自己没有这样想过,是一个绝美的思想。
不过再往下,这种理论的发展就难产了。
因为它算出来的电子的电荷和质量跟实际测量的差的十万八千里。加上其他的一些毛病,所以这种假说逐渐被冷落埋没。
不过这种引入额外维度和处理额外维度的思想却流传了下来,逐渐被弦论和一些额外维度相关的理论模型继承。
超弦理论的历史:
在这里先简单介绍一下超弦理论,为后面我们所要讲到的膜宇宙模型以及弦景观做一下铺垫。
超弦理论最早并不叫超弦理论,而是弦理论。不过为了方便以下都简称为弦论。
最早的弦理论并不是像现在宣称那样是万物理论,它的引入仅仅是为了解释在强相互作用下粒子散射,求散射振幅。
可以说,弦论起源于对于强相互作用的研究。
上世纪60年代后期,加速器上发现了非常多的共振态粒子(一类不稳定,寿命非常短的粒子,特点就是碰撞截面在某一个质心能量标度附近有一个凸起来的峰状图像,而且在这个标度附近的碰撞截面,对于能量的依赖性非常大,具有共振现象,故而早期被称为共振态。有确切的自旋,同位旋,质量等等,但是存在的寿命非常短,而且只出现在在强相互作用主导下的粒子散射上。所有的共振态粒子都是强子)。
然而这些共振态的散射振幅(或散射截面)却不能很好地用当时的场论方法计算出来。
这些共振态粒子的散射振幅或者是散射截面满足一种对偶性(这里所谓的对偶性姑且可以理解为:表面上用不同的理论模型去描述,但实际上会导致相同的物理结果)。
这种对偶性就是s-t对偶性。换句话说,就是共振态粒子的散射截面的s道贡献等于t贡献。
这里先解释一下,什么叫s道贡献和什么叫t贡献。它们是这样定义的,在粒子散射过程中,如果两个散射粒子先结合成第三个粒子,然后这第三个新粒子再衰变成两个粒子,那么这个过程将称之为s过程。如果并不是先结合产生第三个新粒子,而是通过交换一个粒子发生反应,那么这个过程将被称为t过程。
因此,显而易见,这两个过程的贡献绝不相同,至少表面上来看不相同。
用当时的量子场论方法计算也是这样,然而60年代的实验表明,很多共振态粒子的散射振幅都满足这种对偶性。所以当时的量子场方法并不能很好地解决如何去计算这些粒子的散射截面问题。
不过不用慌,正所谓理论模型不行,经验公式来凑。
在1968年,一位在麻省理工学院工作的意大利物理学家韦内齐亚诺在无意之间翻看数学手册的时候,发现了一个古老的数学公式——欧拉β函数。偶然发现古老的函数似乎可以去描述那些共振态粒子的散射。
很快就搞出来了计算这些共振态粒子散射截面的经验公式,韦内齐亚诺模型(具有四个粒子的散射模型),他自己压根不知道为啥会这样。
一开始,韦内齐亚诺公式只能解决一两个粒子散射,有很多粒子参与的散射它并不可以解决。不过他的工作算是一种开创,吸引很多人来扩展他的结果。
后来,美国理论物理学家伦纳德·萨斯坎德研究发现这个韦内齐亚诺公式其实描述的是一种一维振动的弦之间的散射而并不是粒子之间的散射。
陆续有人发文章认为韦内齐亚诺公式可以表征为弦的散射振幅。
这就吸引了一大波人做弦论,来研究强相互作用。
人们发现,韦内齐亚诺公式中,有无数个中间粒子态。
通常粒子散射分为三个部分,分别是初态,中间态和末态。初态和末态是可观测的,中间态是不可以观测的。
比如两个电子之间的散射,初态和末态均是可观测的电子,而中间态粒子就是他们交换的虚光子,也就是传递电磁相互作用的虚光子。
所以这些中间态的粒子,它的质量和自旋都可以任意大。在这中间人们发现一种质量为0,但是自旋量子数为2的中间粒子。现在我们一眼就知道这与引力子很像,但是在当时没有人注意到这一点。
这样很多人被吸引过来用这种弦图像去研究散射振幅的计算技术。
的确,当事人们找到了一个计算高圈图的工具,也是唯一一个,那就是光锥规范下的技术,但是也仅仅适用于玻色子弦之间的。
但是,如果要保证整个理论的自洽性,而且保证一些基本的对称性,比如洛伦兹对称性不被破坏,当然也要保证一些基本粒子质量为零,比如光子,因此就必须假设这些玻色子弦是在26维时空中的。
而且是会产生一类无质量的粒子,快子,它更多的物理意义其实是整个体系基态的不稳定性,而并不是超光速粒子。它就相当于沙丁鱼群中的鲶鱼一样,让整个沙丁鱼鱼群(物理体系)不稳定,包括后来提出的真空衰变也是基于这个(确切的说是可以作为某种模型)。
然而不久后,盖尔曼提出了QCD理论,一种完美的场论。非常成功且圆满地解决了包括共振态和散射振幅等等之前令人头疼的强相互作用的问题。
因此,弦理论在强相互作用上被量子色动力学掐死,渐渐消失。
尽管弦理论看似已经死去,但是还是有几个人在坚持做弦论,比如加工理工学院的施瓦兹,英国人格林(不是那个美国的布莱恩·格林),法国人舍尔克。这个时候大部分人都认为弦论是死掉的理论,没有必要在这方面浪费时间。
还记得我们之前说过那个自旋和质量都跟引力子很像的中间态粒子吗?它在一方面也为弦理论续了一波命。
在1980年左右,施瓦兹他们惊奇地发现,这个自旋为2,质量为0的粒子非常像引力子,于是他们假设,也许弦理论并不是描述强相互作用而是描述引力相互作用的一种可行的理论。结合刚提出来不久的超对称建立了超引力理论(超引力就是引入超对称的广义相对论)。
这里要简单讲一下什么叫超对称理论,超对称理论在不同领域,有不同领域的版本,这里只是其中之一。
超对称理论:
它是玻色子和费米子之间的对称性,通过超对称变换一个费米子体系可以变换成玻色子的体系。
超对称变换你可以当做是在某种特殊的抽象的数学空间——超空间中的变换或者旋转。
超空间的坐标由普通的数和格拉斯曼数共同组成。所谓的格拉斯曼数就是一种代数结构,它满足以下几个条件:
ab=-ba(反交换对称性)
αα=0(平方为零)
下面我们讲讲这种理论的发轫。
众所周知,基本粒子或者说粒子分为两大类,一种是玻色子,用于构成场与传递相互作用;另一种则是费米子,用于组成各种物质的基础。
判别他们的唯一标准就是自旋量子数。
自旋量子数或者自旋当作一种量子数或者是粒子在内部空间也就是自旋空间中的旋转(这种自旋空间是不同于时空的,姑且可以把它当做一种数学上的抽象空间),是可以用相同的数学工具去描述的。
自旋的方向在自旋空间中是任意的,但是在三维空间中只有两个取向,分别用“+”、“-”号标记。
一般对于玻色子和费米子的定义是这样的:
自旋量子数为整数倍h-拔的粒子被称之为玻色子,它符合玻色——爱因斯坦统计分布规律;自旋量子数为半整数倍h-拔的被称为费米子,它符合费米——狄拉克统计分布规律(经典粒子符合玻尔兹曼——麦克斯韦统计分布,当不考虑量子效应的时候,上面两个统计分布就会退化成玻尔兹曼——麦克斯韦统计分布)。
其中h-拔被称为约化普朗克常量或者狄拉克常量。
玻色子和费米子的概念很广,不仅仅适用于基本粒子,甚至是复合粒子也可以。
比如一对夸克构成的介子,三个夸克构成的核子(中子和质子),甚至是原子核。比如之前的玻色——爱因斯坦凝聚态,甚至是费米——狄拉克凝聚态都是原子核的凝聚。只不过有些原子核是玻色子,有些原子核是费米子。
不过原子就不可以适用于这个概念,因为原子并不是一个复合粒子体系,它的内部自由度不为零,电子在高速运转。
最早做超对称这项工作的就是上世纪60年代末,前苏联物理学家高尔芳,他的目的是寻找一种联系玻色子和费米子体系之间的对称性,他当时是为了解决弱相互作用。
不过很可惜这样工作没多少人注意,尤其是1967年之后,温伯格发表了关于弱电统一理论的文章。
而欧美物理学家则是另一个动机,研究弦理论。在1971年左右,还在费米工作室工作的皮埃尔·拉蒙考虑在弦论中引入带半整数自旋的激发态也就是费米子。
前面我们说过在超对称理论中,超空间的坐标由普通的数和格拉斯曼数共同组成。所谓的格拉斯曼数就是一种代数结构,其中有一个性质就是反交换对称性,而费米子的波函数也具有反交换对称性。
因此,在拉蒙的理论中,弦的激发态是费米子,但是也包含原有的玻色子。弦的运动产生的轨迹叫做世界面(这在后面也叫做P膜),它包含着玻色子的场也包含着费米子场。不过主要研究的还是费米子弦。
就这样提出了超对称的理论,在弦理论中,将玻色子和费米子联系在一起。
不过在当时也没有得到重视,而且不久后被费米实验室开除了,尽管拉蒙用费米实验室的名字命名这个新的领域。
让我们回到施瓦兹的工作,他引入超对称理论之后,并结合这个引力子,建立起来了超引力理论。
从此,弦理论首次作为量子引力理论而登上舞台。而且超引力有着大家非常想要的东西,比如,普通引力的直接量子化被证明是发散的,不可重整的,不仅发散项是无穷多的,而且无法分离(无法用正规化),更别提引入抵消项(无法用重整化)。
然而惊奇的是超引力是有限的,至少在展开到第八项的时候,往下再计算太困难了。
而且在弦论中,没有点粒子之间是发散的,因为一维的弦是有尺度的,不会出现点粒子的自能或者其他力学量的无穷大。
因此,这些无穷项是不会出现的,重整化也就变得无关紧要。因为没有烦人的无穷大还有处理无穷大的方法,因此,加入超对称的弦理论显示出理论该有的优美和自洽性。又吸引了一波人做这项工作。
这是弦理论的第一次大革命,也掀起了一波热潮。
但是很多人都在一起做,大家都有自己的方向,于是又产生了5种超弦理论,这五种超弦是:I型,IIA型,IIB型,杂化I型,杂化IⅠ型。弦论学家们发现了这几种自洽的弦理论,但谁也无法说明这五种弦理论哪一种是正确的。他们表面看起来没有任何关系,甚至是有点敌对。
因此,大家都想证明自己是正确的,但是都无法证明。于是僵持又开始了,大家不知道哪种弦理论是正确的,所以说弦论开始停滞不前。
幸运的是,在1994年,文科生爱德华·威腾证明,五种超弦彼此是对偶的,还记得我们前面说的对偶是什么意思吗?它们虽然表面看起来不一样,其实是可以导致同一个物理结果。
爱德华进一步认为它们只是一个M理论(膜理论或者矩阵理论)的五种不同的极限理论。
对偶性再次出现在人们眼前,这一次对偶性被证明是很重要的。直到今天,一部分研究弦理论的人,只是为了专门研究对偶性。
于是这又掀起了研究弦论的一波浪潮,这也是第二次革命的发起。
在1995年,Polchinski提出了D膜的思想以及对偶性用D膜的表达,D膜它是开弦端点的地方,开弦两端终结于D膜上,而这个膜满足狄利克里边界条件(开弦的某个坐标在端点必须是固定的),所以叫D膜。
这就是弦理论大概的发展历史。
早期弦理论主要是玻色子弦理论,之所以叫这个名字,顾名思义,只能解决玻色子。
我们都知道弦论中,基本假设就是所有的基本粒子都是弦的振动产生的。基本粒子之间的区别是因为不同弦振动的模式和振动方向的不同。
然而,基本粒子分为两大类,玻色子和费米子,因此弦论所面临的第一个问题就是必须可以解释为什么基本粒子会分成这两类。
不过早期弦论只能解决玻色子的生成问题,它无法解决费米子的生成问题。
但是引入超对称之后,就可以完美地解释费米子生成问题,因为人们发现有些膜存在激发态,而且表现出来的粒子并不是弦振动产生的,所以,并不是所有粒子都可以通过弦振动产生。但是我们没有观察到这类粒子。
对于弦理论并不想介绍这么多,只是为了下面的膜宇宙高维空间以及弦景观做铺垫。
弦论中,对于额外的高维空间也就是超过三维空间的,人们往往就是把它紧致化处理,大尺度上我们是看不见这些超过三维空间的维度,它只有在小尺度上才可以存在。而弦理论认为这个小尺度是普朗克度(类似于之前介绍的卡鲁扎——克莱因五维理论也是这样要求额外维度的尺寸)。
弦理论认为,我们通常的宇宙是三维空间加上一维时间,而多余的六维或七维空间被紧致化在卡拉比——丘流形上(类似于我们之前举的一维的线和二维的吸管的例子,在那个例子中,二维作为额外维被紧致化在一个具有一定半径的圆柱上。卡鲁扎-克莱因五维理论第五维作为额外维被紧致化在一个有具有一定半径的圆环上。而在弦论中,这里的圆柱体,圆环被卡拉比-丘流形充当)。
之所以引入这么多高维空间,也仅仅是为了理论上的优美和自洽以及满足一定的基本的物理定律和现象(就像之前说的,包括一些已知的零质量粒子,比如光子,要保证弦的激发产生的光子质量为零,同时也要保正洛伦兹不变性)。
我们下期继续介绍。
参考引源:
《引力论与宇宙论》美国,斯蒂芬.温伯格。
《天体物理概论》向守平。
《超弦史话》李淼。
《额外维模型与对称性破缺》兰州大学,李庆、任继荣。
《探测额外维的实验设想及膜世界图景的研究》大连理工大学,罗峰、刘宏亚。
《通向实在之路-宇宙法则的完全指南》英国,罗杰.彭罗斯。
《时空的维数》李新洲。
《弯曲的旅行-揭开隐藏的宇宙维度之迷》美国,丽莎.兰道尔。
《源自弦景观的有效Quintessence》翟韩豫、申佳音、薛迅。
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会将追究版权责任。】