科普驿站 第二十三期
主题：浅谈庞加莱猜想
科目：数学
难度：C1
讲师：Delta
引 言
1904年，在一篇名为《对位相分析学的第五次补充》的论文中，亨利·庞加莱(Henri Poincaré)提出了一个猜想：在一个三维空间中，假如每一条封闭的曲线都能收缩到一点，那么这个空间一定是一个三维的圆球。
这就是高深莫测的庞加莱猜想。这个猜想究竟想表达什么呢？为什么一个连数学符号语言都没有的、完全用自然语言描述的看似“显然”的猜想能困扰历代整整九十九年的数学家？
今天这篇文章就着重来解释这些问题。
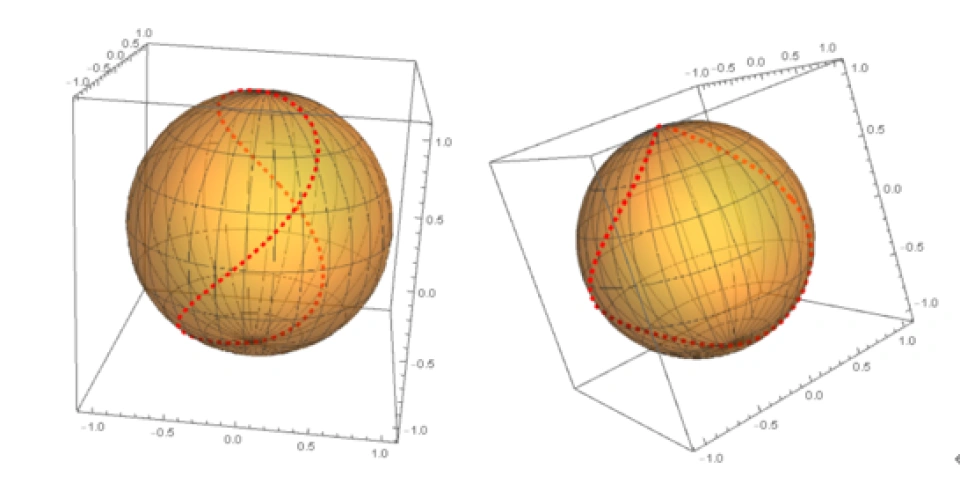
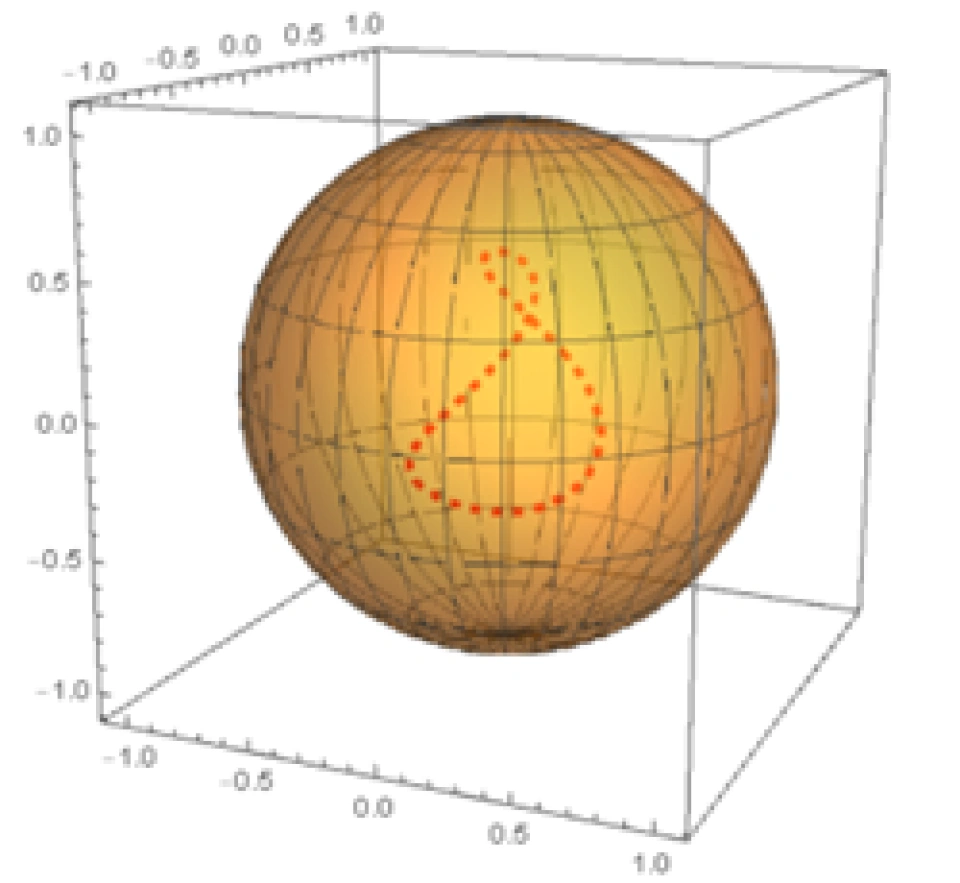
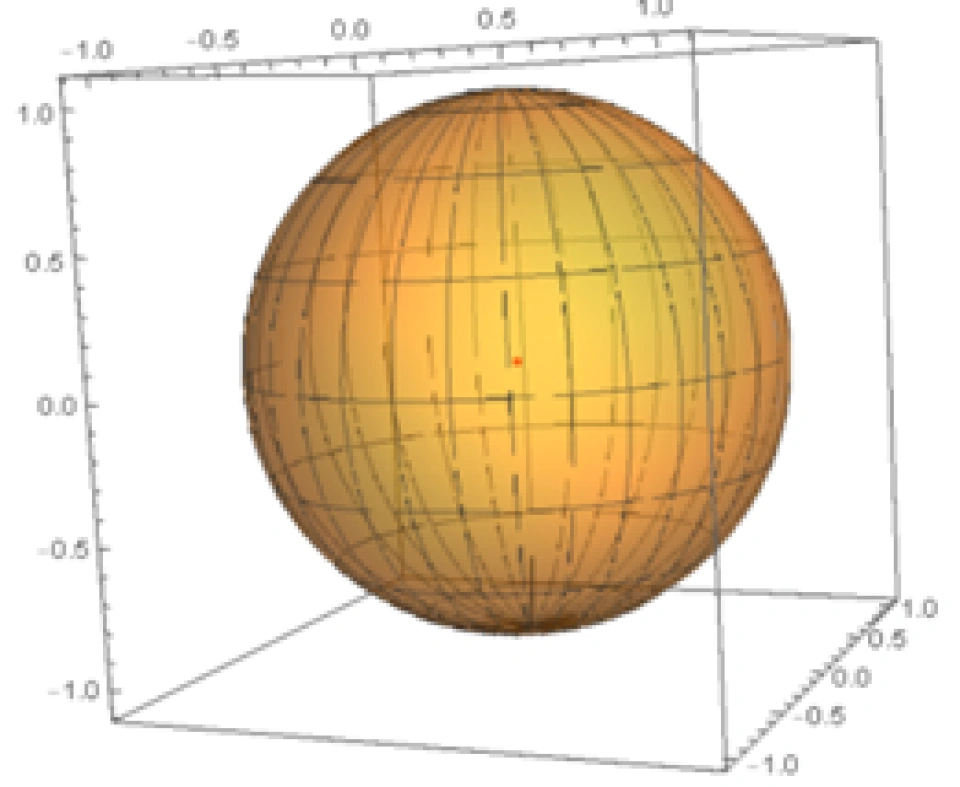
其实这句话的意思并不难理解。我们先反过来，从一个三维球体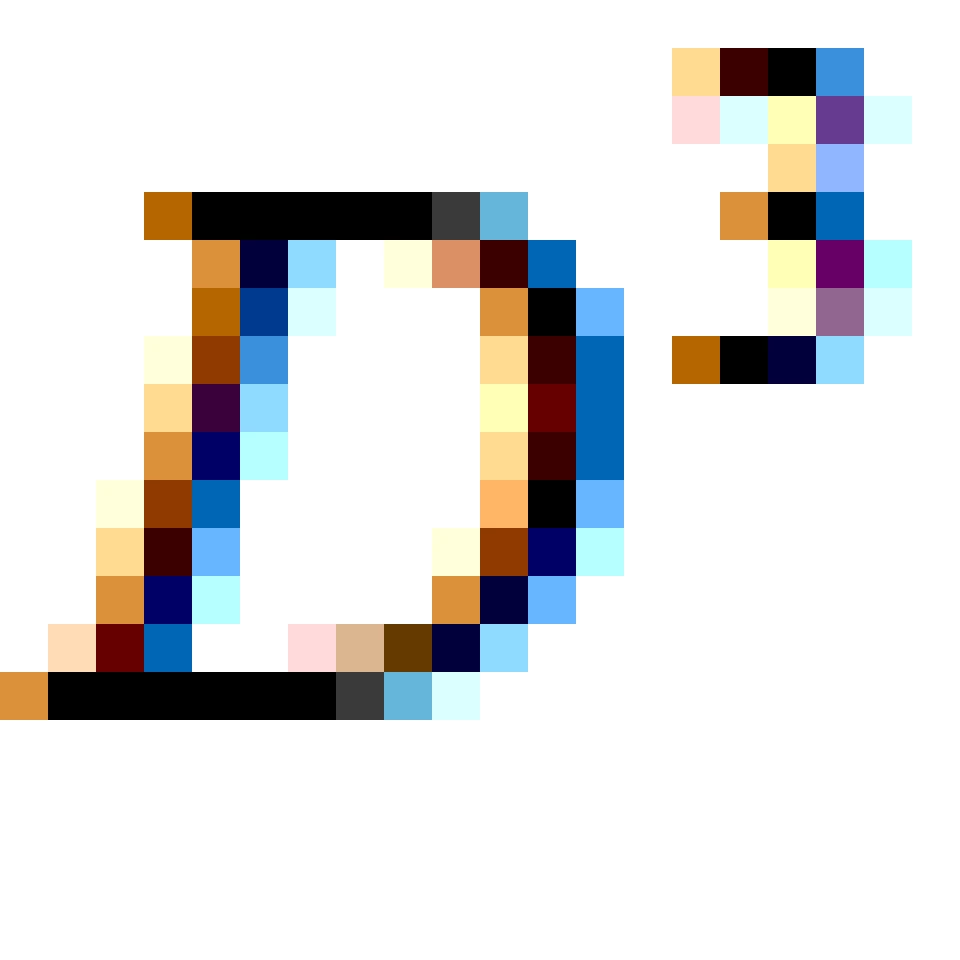
内部的一条封闭曲线开始考虑。下面我们通过数学软件模拟出来这个情形：
其结果为：
现在我们让球内的曲线任意收缩，如图：
最终能收缩成一个点
。
不难看出对于球内的任意一条闭合曲线都是这样。也就是说，我们可以观察出来，在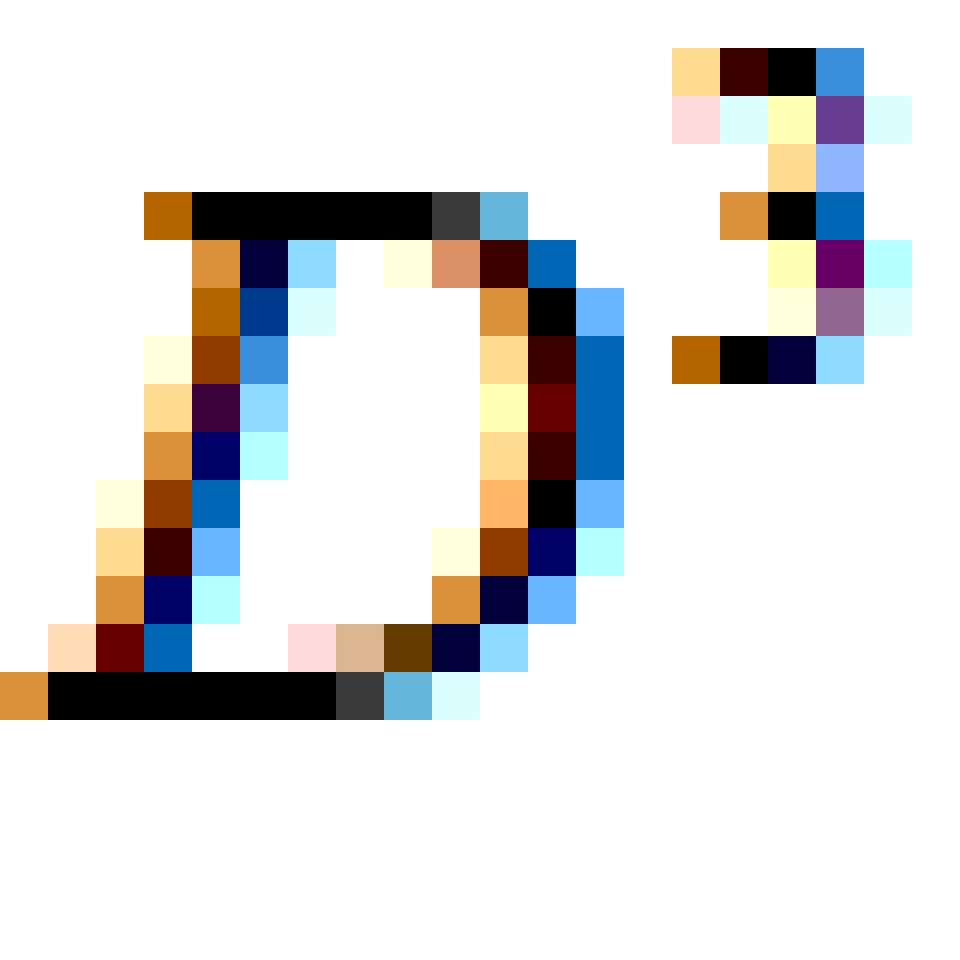
中，每一条封闭的曲线都能收缩到一点。而庞加莱猜想则是把这条看起来显然的定理逆过来，他认为利用每一条能收缩到一点的曲线，能够推导出这些曲线所在的空间的性质。
当然，到这里你可能有个问题：就算能够利用曲线的性质推导出它所在空间的性质，但为什么偏偏是球体？为什么不能是其它形体？
其实不一定是球体，也可以是正方体、长方体，甚至可以是
：
好吧。我承认心形体确实不大可能，除非设计这个空间的人是个可爱的女孩子。
撇开这些不谈，实际上，上面说到的这些形状，专业名词称之为流形(manifold)，通俗地来说被定义为：
局部具有欧几里得空间(Euclidean Space)性质的空间。
什么叫做欧几里得空间？
这样讲吧，一维的欧几里得空间就是（实）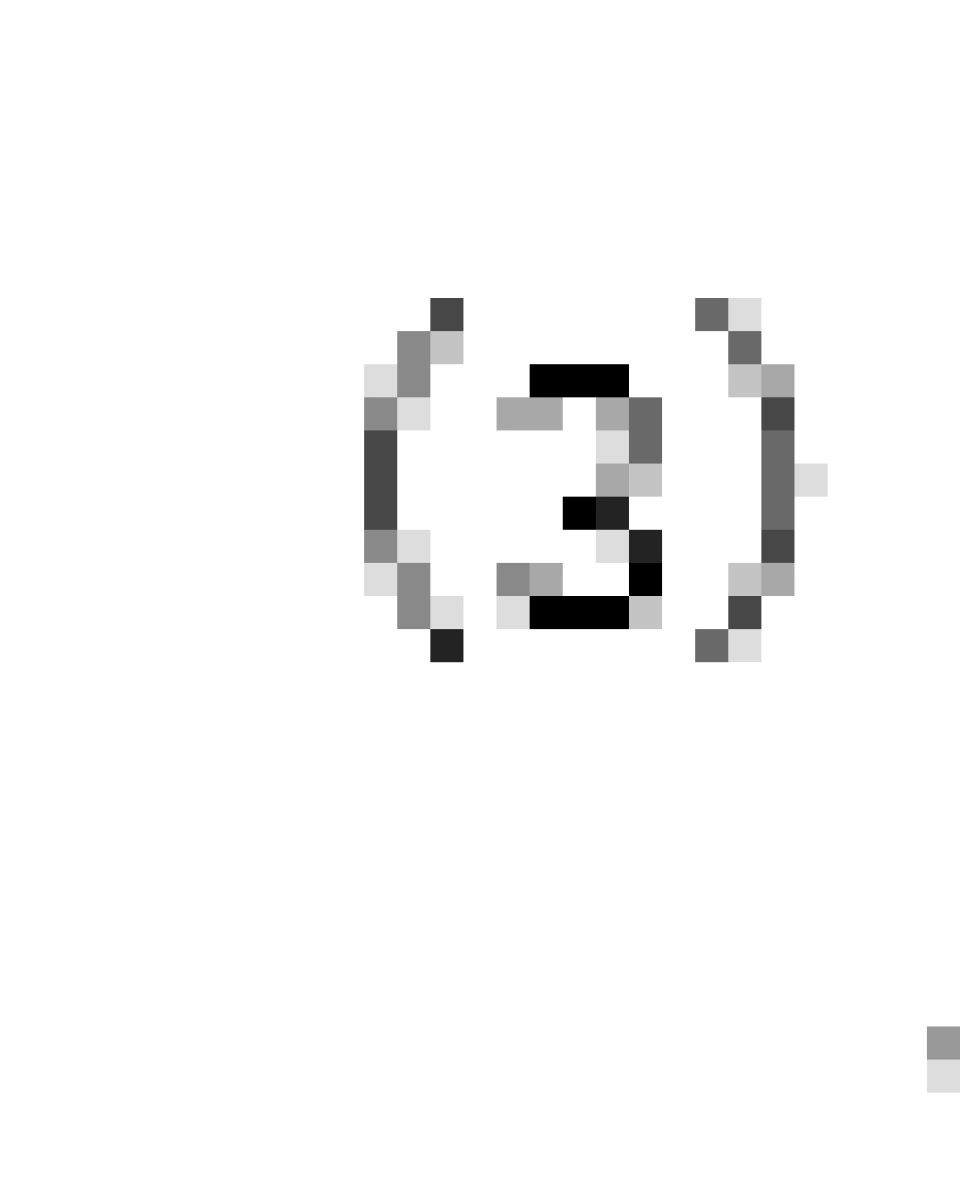
直线，二维的就是平面，三维的就是立体，跟我们日常生活中所认识的一样。
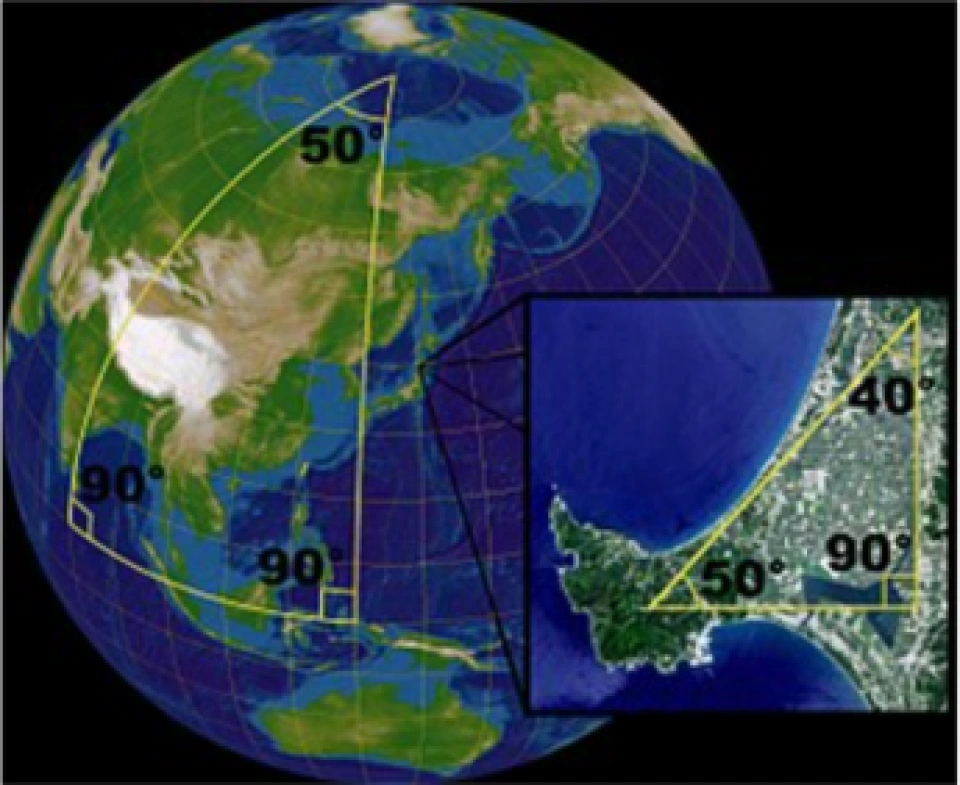
在此基础上我们来理解流形。先来一个最贴近我们的例子：现在人类基本上都知道地球近似是一个球体，也就是说它的表面是一个球面，那我们平常生活中出行能感受到这个球面的曲率吗？
“大三角形”虽然是曲边的，
但右下角非常小的三角形就和平面上一样了。
（原图来自维基百科）
显然不能，这是因为在局部上，球面是等价于平面的。这也是为什么古人认为地球是一个大圆盘，因为在不观察月食现象、做环球旅行或是其他实验的情况下，如果不能上太空，人类又无法直接从宇宙中直接观察到地球的整体，只能看到局部，那么自然无法判断地球的真实形体。这就叫做局部具有欧几里得空间性质，也因此我们认为地球的表面是一个二维流形，因为它局部具有平面的性质。
更“数学”一点来说，如果一个空间能够以某种方式投影成n维欧几里得空间，那么这个空间就被称作n维流形。真正的数学定义其实是这样的：
设M是Hausdorff空间，若对任意一点x∈M，都有x在M中的一个邻域U能与m维Euclid空间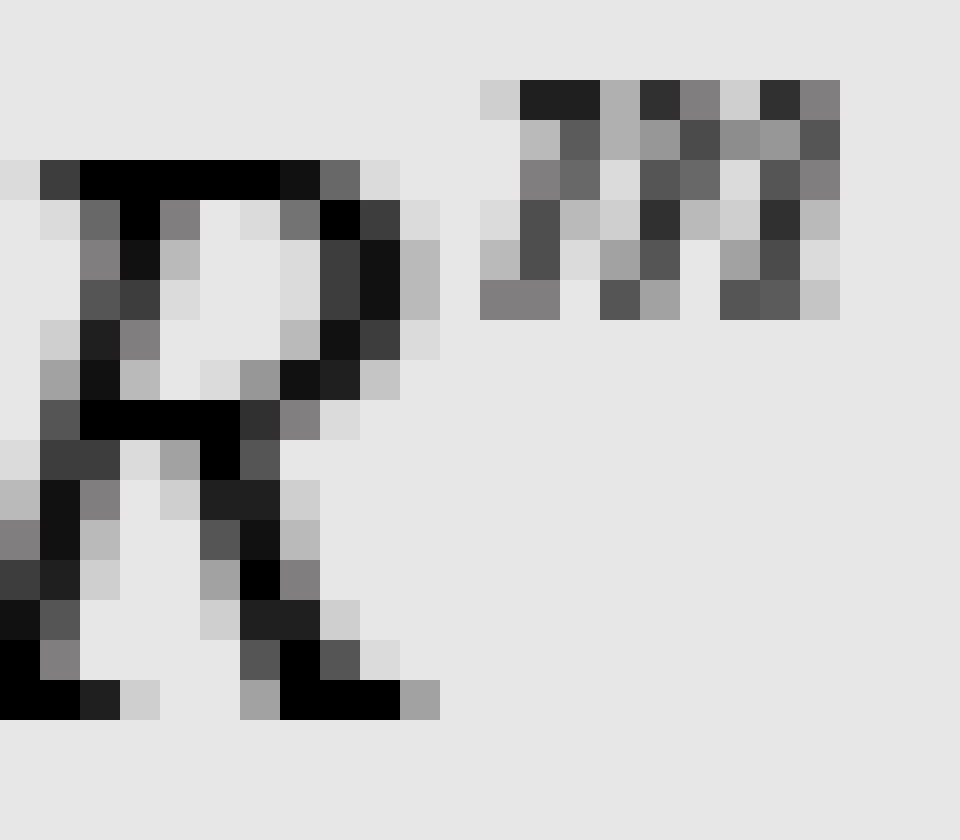
的一个开集建立双射（同胚于），就称M是一个m维流形。
而我们前面提到的球体、正方体或是心形体，它们都是三维流形。这里我们要说，它们在点集拓扑上(General Topology)都是等价的。这里的等价有两种概念，第一是同伦(Homotopy)等价，第二是同胚(Homeomorphism)。也就是说，在拓扑学家(topologist)的世界观中，球体和你所说的正方体、长方体其实都是一样的，没有任何区别
。这就是为什么我们说“不一定是球体”但却用球体来描述该猜想，因为它们在拓扑学里都是一样的。（这里没有压迫，人人平等！）
那么什么是拓扑学？在这里我们引用北大尤承业教授在《基础拓扑学讲义》的引言中所写的内容：
“什么是拓扑学？”这是许多初学者都会提出的问题。拓扑学是一种几何学，它是研究几何图形的。但是拓扑学所研究的并不是大家熟悉的普通的几何性质，而是图形的一类特殊性质，即所谓“拓扑性质”。于是，要了解拓扑学就要知道什么是图形的拓扑性质。然而，尽管拓扑性质是图形的一种很基本的性质，它也具有很强的几何直观，却很难用简单通俗的语言来准确地描述。它的确切定义是用抽象的语言叙述的，这里还不能给出。
……
以上几个问题显示出几何图形的一类特别的几何性质，它们涉及到图形在整体结构上的特性，这就是“拓扑性质”。显然，它们与几何图形的大小、形状，以及所含线段的曲直等等都无关，也就不能用普通的几何方法来处理，需要有一种新的几何学来研究它们，这个新学科就是拓扑学。也有人形象地称它为橡皮几何学，因为它研究的性质在图形作弹性形变时是不会改变的。
由于篇幅有限，在该书提到的“几个问题”中我们仅选取Euler多面体定理进行详细的叙述，另外的两个问题分别是“七桥问题”和“地图着色问题（四色问题）
”，感兴趣的读者可以查一查。
对于Euler多面体定理，相信大多数人在学习立体几何的时候一定早有耳闻。它说的是：
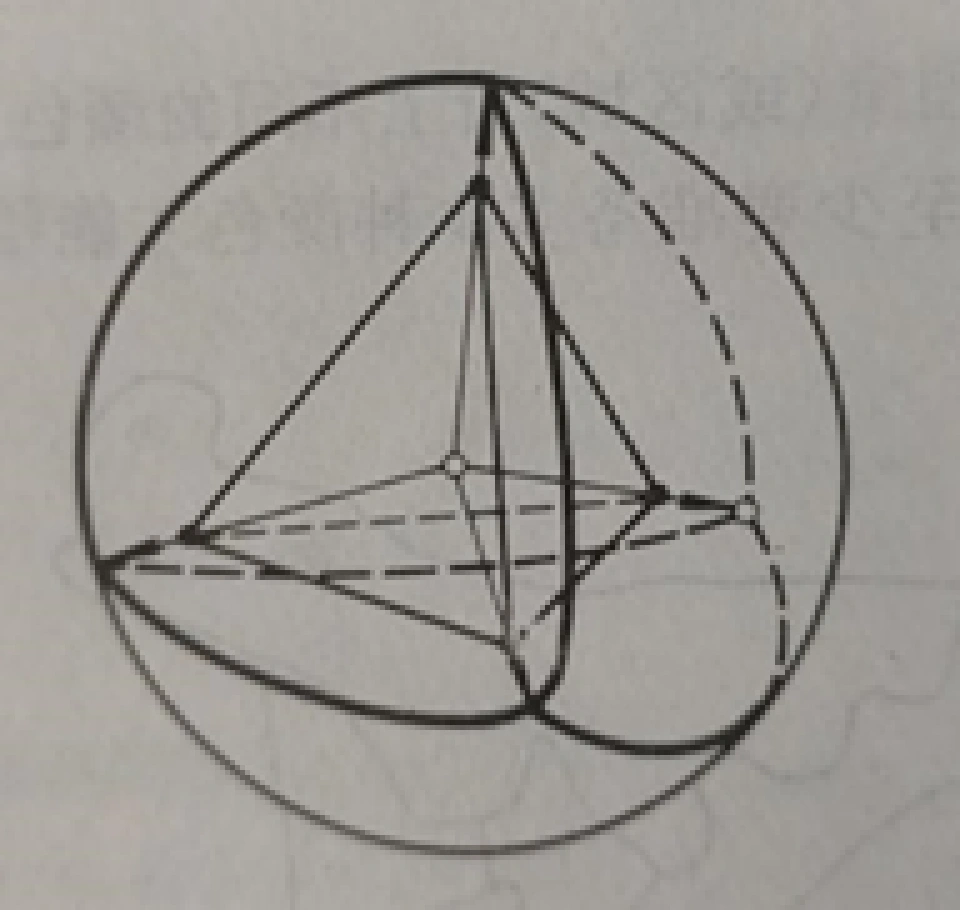
然而，既然我们需要的是在弹性形变时不会变化的性质，我们就得抛开多面体来考虑。现在把凸多面体放进一个大球体，并使球心在多面体内部。接着从球心做中心投影，把凸多面体的顶点映射成球面上的节点，棱映射成球面上的曲线（被称为枝）。这些节点和枝构成球面上的一个图，它把球面分割成f个面块，有l条枝和v个节点。如图：
这个图满足：
(1) 每条枝的端点是两个不同的节点；
(2) 不同的枝不会相交于内点；
(3) 每条枝不会自交。
在这个意义上，欧拉定理可以推广为：
球面上一个连通的图的节点数v，枝数l以及它分割球面所成的面块数f满足公式
当球面变形时，可以看出f、l和v这三个数并不会变化，所以对变形的球面比如椭球面，或是任何闭的单连通二维流形（这里的闭表示封闭）这个定理仍然成立。
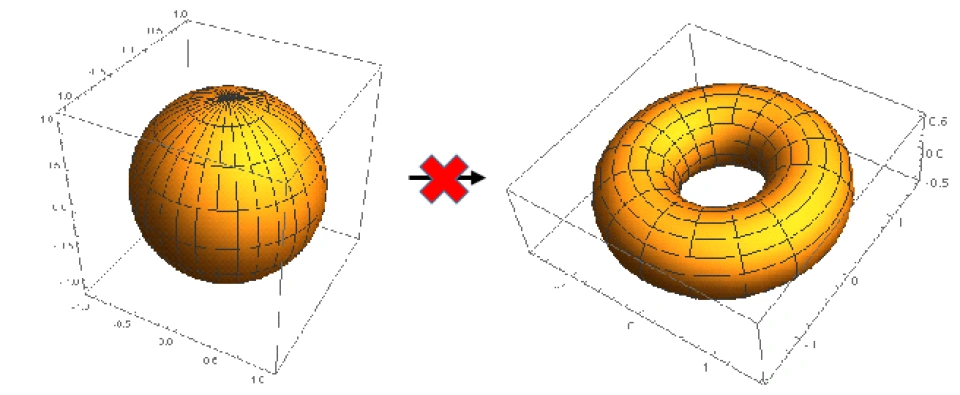
要注意，我们这里说的变形，是一种连续的过程，是不发生粘连或者撕裂的变形。在这种变形下，你不可能把一个球面变成一个环面
：
否则你必须撕裂这个球面然后再以其他的形式粘连，或者直接把球面的两极下压至粘连再撕裂。这也就意味着，球面和环面之间的一些拓扑性质是不同的。比如上文提到的欧拉定理，如果在环面上存在一个连通的图，那么它必然满足：
环面上一个连通的图的节点数v，枝数l以及它分割环面所成的面块数f满足公式
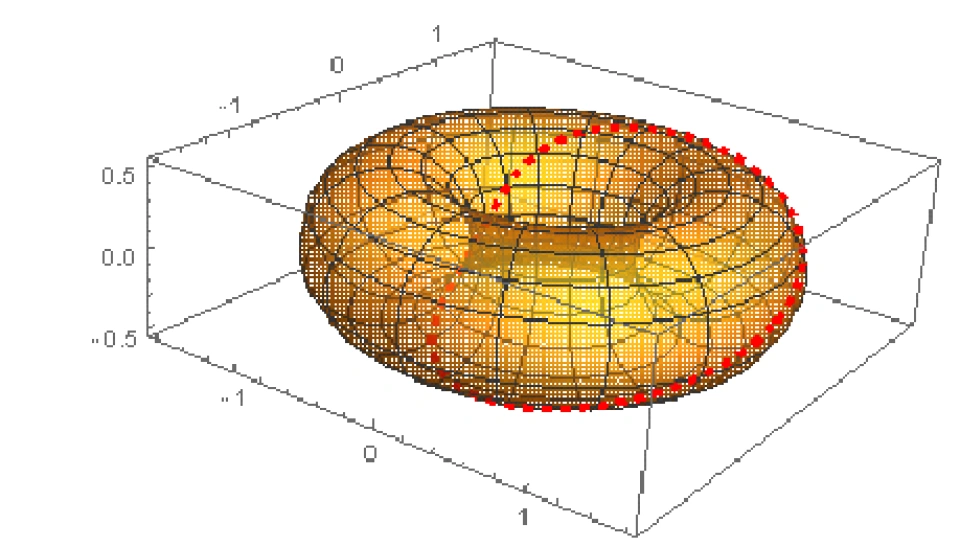
不仅是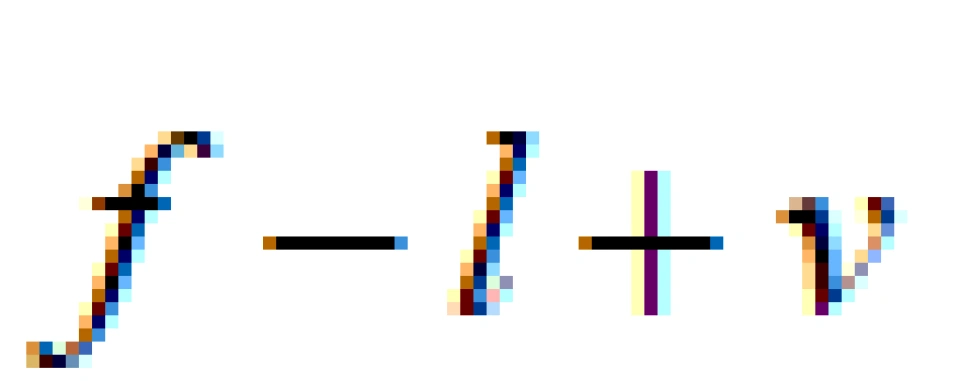
的得数，还有其他许多不同的性质。比如，我们不难看出，环面比球面在中心多了一个洞，这意味着如果我们像开头那样在环面的内部（我们一般把它叫成甜甜圈）任意画一条闭合的曲线，这条曲线不一定能收缩成一个点
：
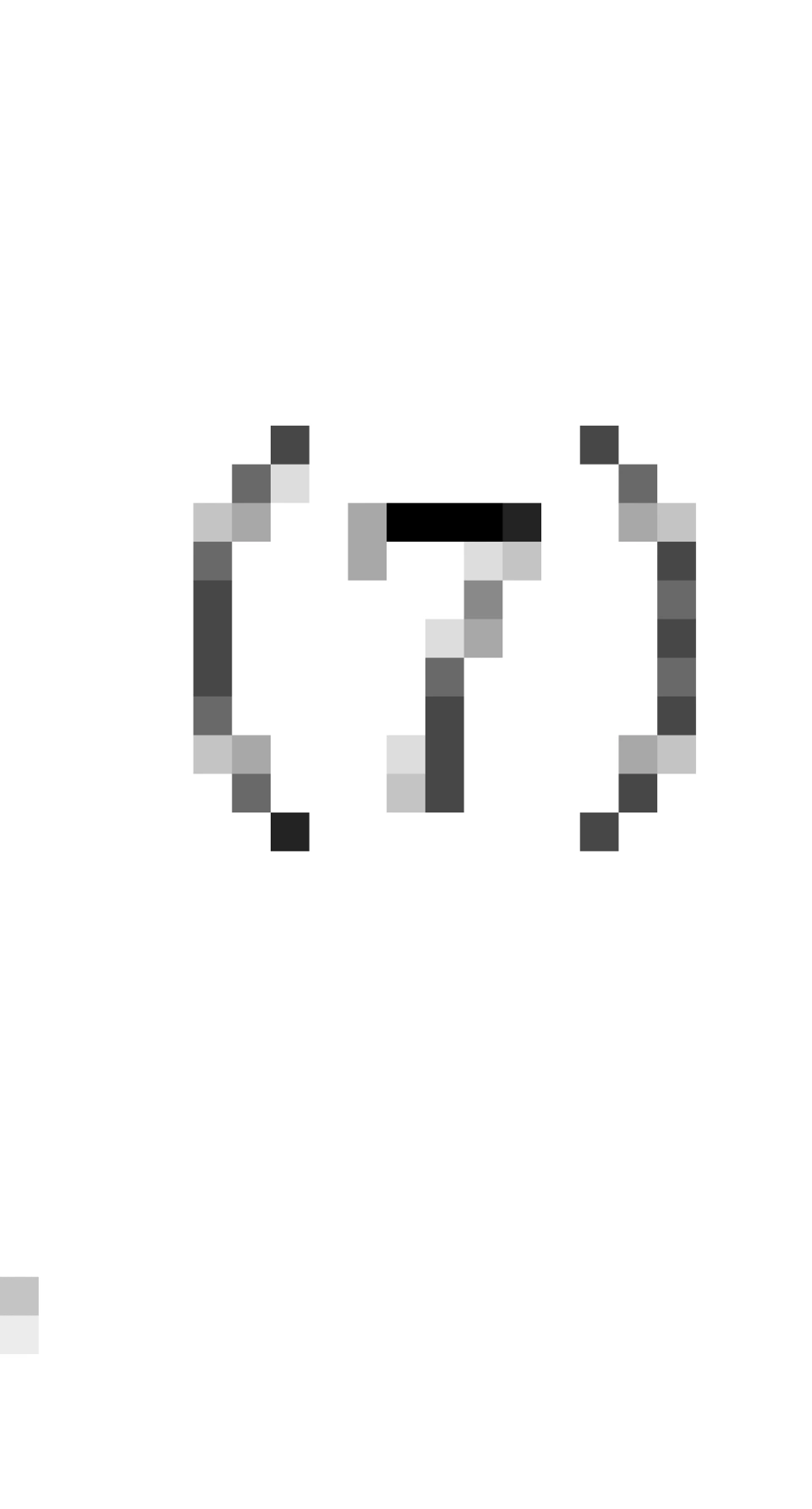对于上面这种情况，不难看出这条曲线在收缩的时候会被中间的孔洞挡住，从而变成孔洞的形状而无法收缩成一个点。我们把这种情况叫做一维多连通（非一维单连通），把孔洞的个数叫做亏格(genus)。亏格也是一种拓扑性质。
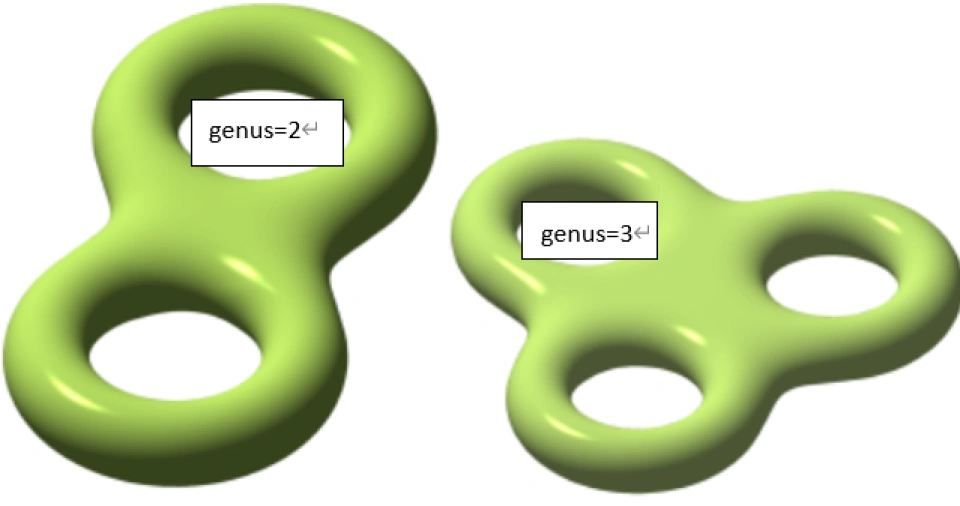
球面显然是一个零亏格曲面，而环面则是一亏格。而对于亏格更大的曲面，比如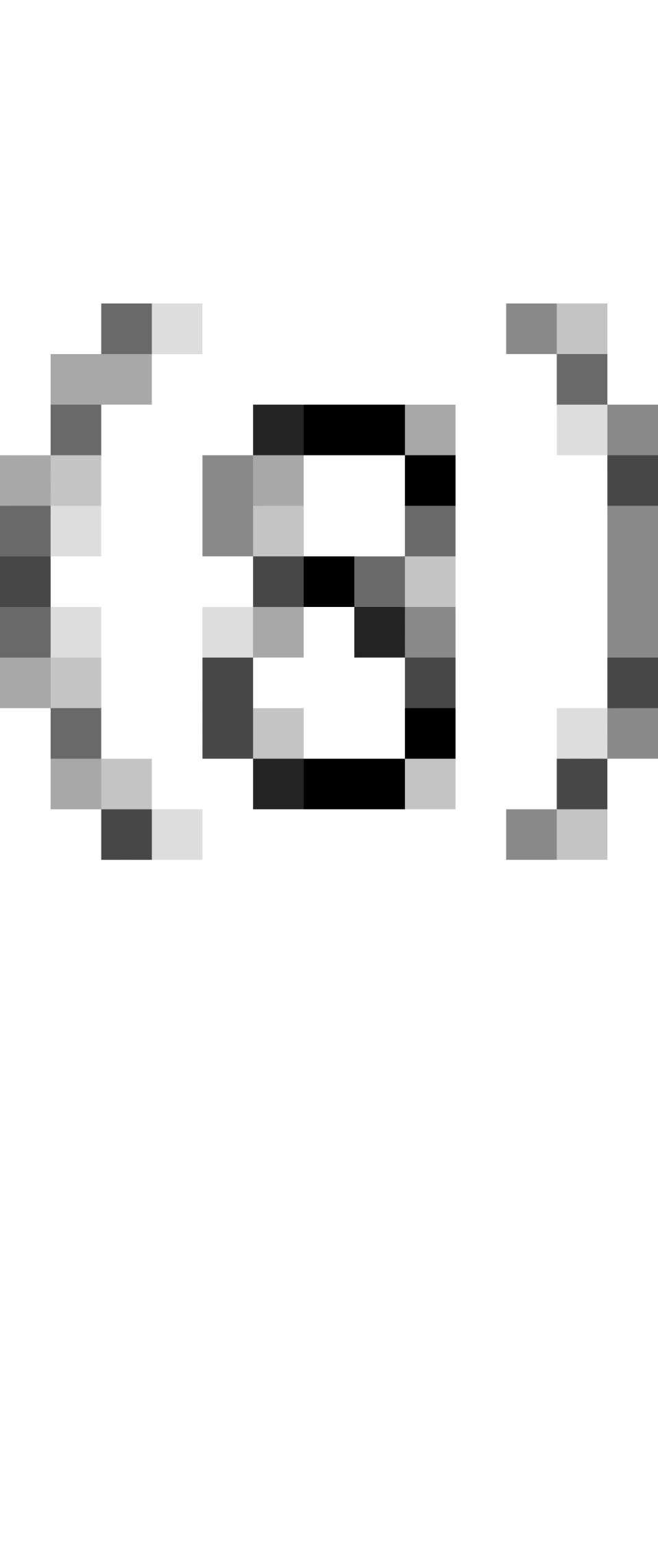
：
它们的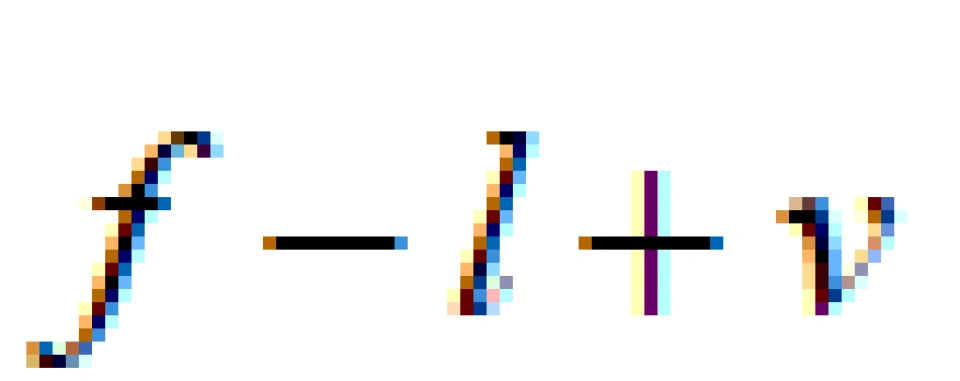
是一个负数，我们把这个由曲面本身的性质决定的数叫做Euler数。
注意到，我们在上文对拓扑学的介绍中多次提到了一种连续的变形，这种连续的变形就是我们在开始介绍拓扑学之前就已经提到的两种等价：同伦和同胚。这两种等价关系都不会改变在上文提到的两个性质，因为亏格和Euler数（Euler示性数）都是同伦不变量，而同伦不变量一定是拓扑（同胚）不变量。
然而，实际上，第二种等价——同胚要来的比同伦更严格一些。同胚的定义是两个空间内所有的元素都能构成双射，也就是一一对应，并且这个映射 及其逆映射（双射一定存在逆映射） 都是连续的，分别表示几何意义上的不撕裂和不粘连。同胚变换不会改变一个流形的任何拓扑性质。
但同伦会改变。这里我并不准备给出数学上关于同伦的绝对定义，它要比同胚的双射难理解的多，因为它描述的是基于空间内存在两种映射的连续变换，再根据恒同映射定义的。尝试理解这个就不叫科普了，所以我准备给大家举几个例子。
针对于同伦而言，一条没有宽度的直线L和一个平面Ω是同伦的，因为显然存在一个映射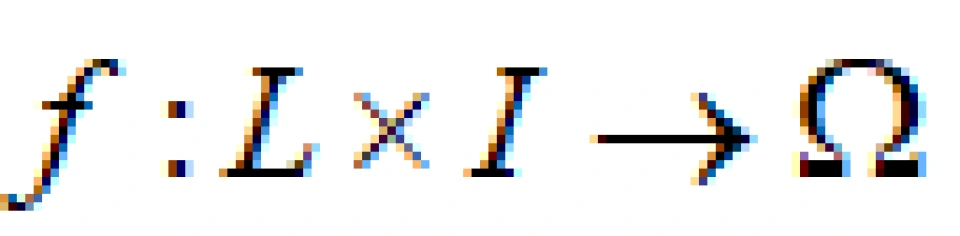
能把直线映射到平面上，但它们是不同胚的。再比如，X和Y这两个字母，是同伦而不同胚的。从这个角度上，我们来看中日关系和中美关系，它们各是什么？
中日关系是同伦不同胚的，中美关系是不同伦也不同胚的。
了解了这些概念之后，我们再来看庞加莱最初提出的猜想：
在一个三维空间中，假如每一条封闭的曲线都能收缩到一点，那么这个空间一定是一个三维的圆球。
我们现在知道，这个圆球是拓扑意义下可以做同胚变换的“圆球”。这是正确的吗？我们好像想象不出其他的情形，但这并不足以说明这个猜想是对的。实际上它是错的，因为它没有考虑流形的边缘。
什么是流形的边缘？
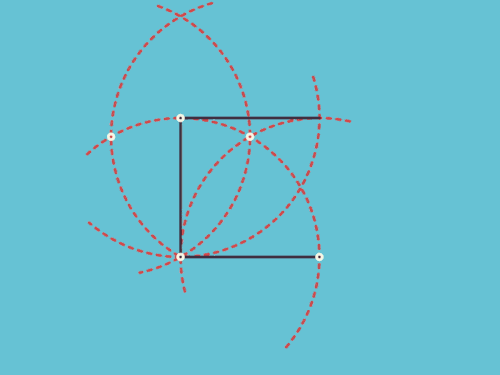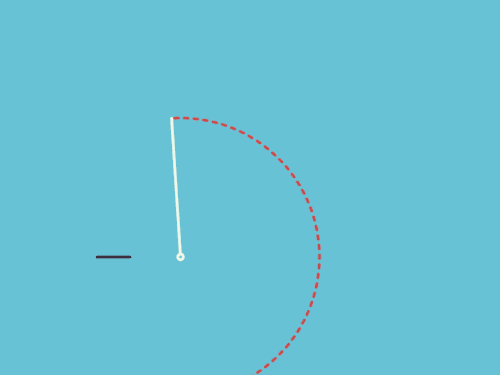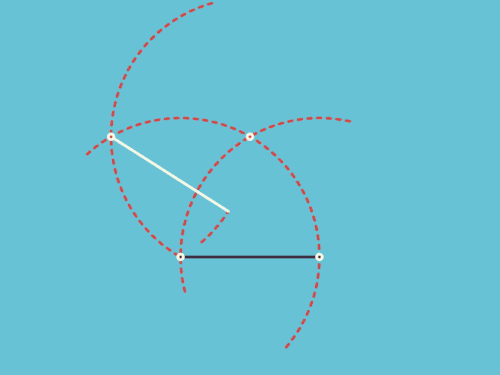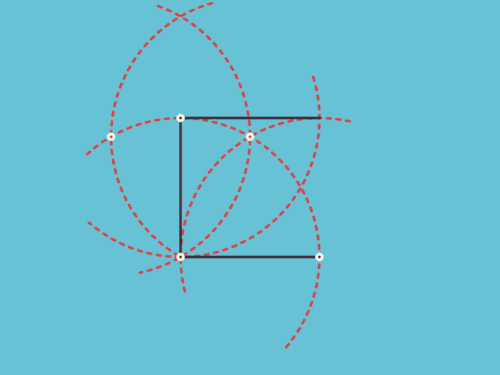
让我们从大家最熟悉的开区间和闭区间开始讨论。事实上，开区间就是一个无边缘的一维流形，而闭区间就是一个带边缘的一维流形。在初高中，我们是怎么用通俗易懂的手段来判断开闭区间的呢？是看这个区间包不包含端点。这个端点就称作一维流形的一个边缘。同样的，如果我们把区间的带边缘问题整体提升一个维度，来研究二维流形，那么我们判断的根据就是这个二维流形包不包含“边界线”。
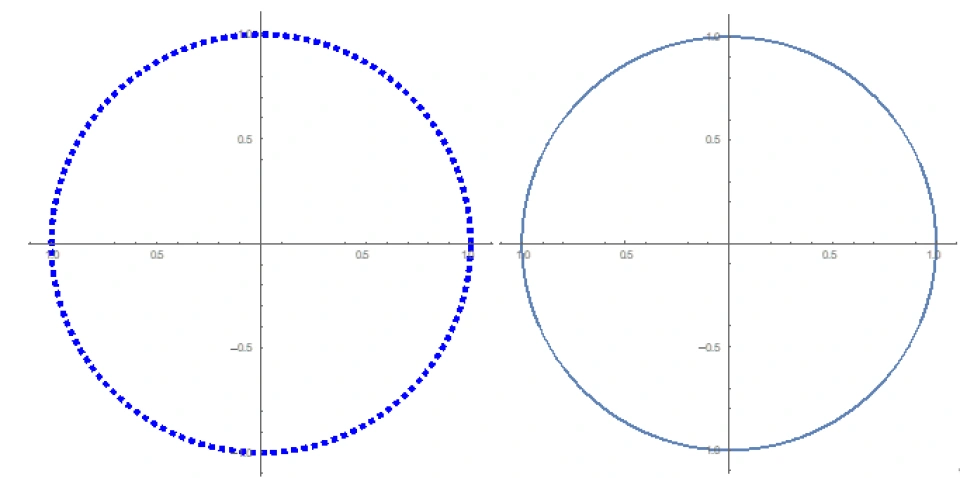
如图，虚线代表不含圆周：
显然，前者是无边缘的，后者是带边缘的。
在这里我们要说明两个问题。首先不能像开闭区间那样按流形是否带边缘称作开闭流形。事实上，开闭流形都是无边缘流形，区别是紧致化的问题。这个问题我们不谈。
其次是圆盘是一个二维流形，所以它的边界线（圆周）自然而然的是在二维空间内，但圆周仍然是一个一维流形，因为它只有一个自由度。任意n维带边缘流形M的边缘——我们记作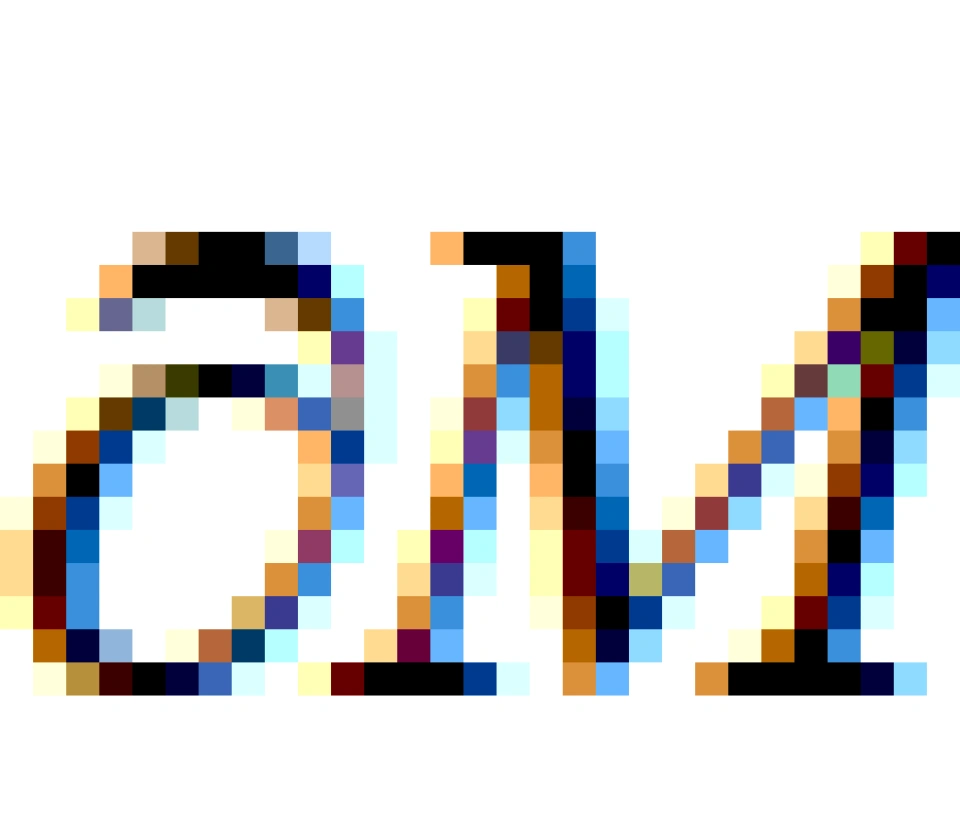
——都是一个
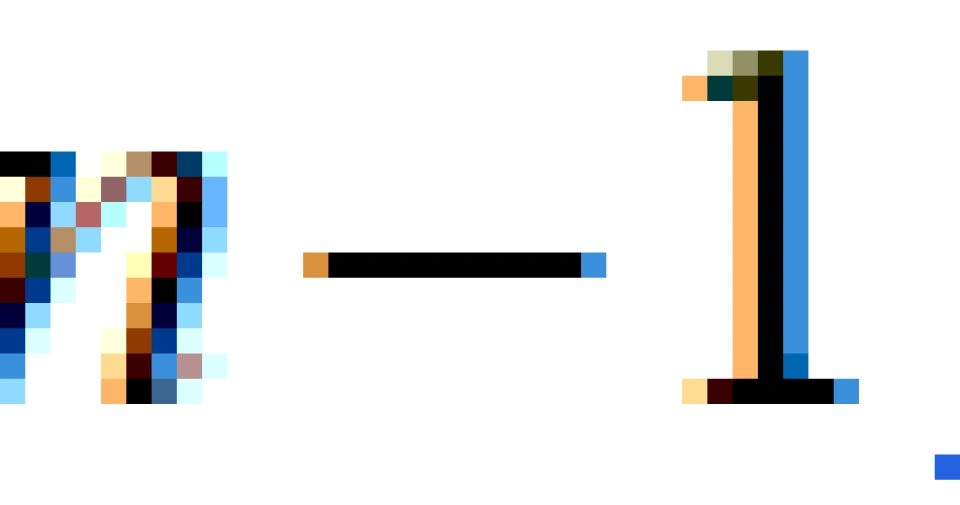维无边缘流形。特殊地，当这个流形
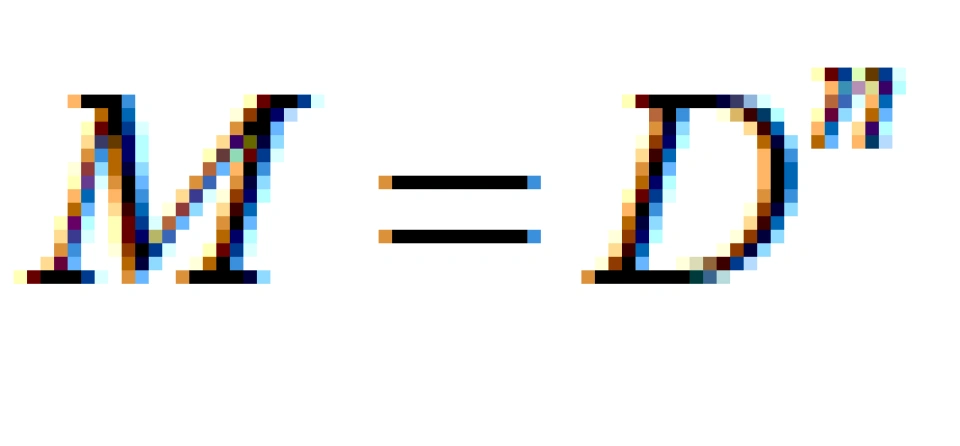为n维球体时，
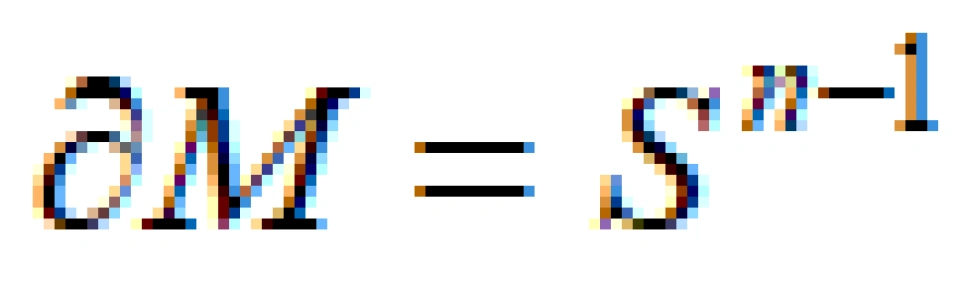为n-1维球面。其中：
显然，一个无边缘三维流形，不能等同于带边缘（球面）的三维球体，所以我们说这个猜想是错的。庞加莱在1905年发现了他叙述中的错误，并对其进行了修改：
任何与三维球面同伦的三维封闭流形必定同胚于三维球面。
或者说：
任何一个单连通的，闭的三维流形一定同胚于一个三维的球面。
这才是真正的庞加莱猜想。
我们刚刚才提过，二维球体（圆盘）的表面是一个一维球面（圆周），而三维球面实际上是四维空间中的东西，它是平铺于四维球体上的一层没有四维“厚度”的膜。也就是说，我们无法想象出三维球面（超球面）到底长什么样子。
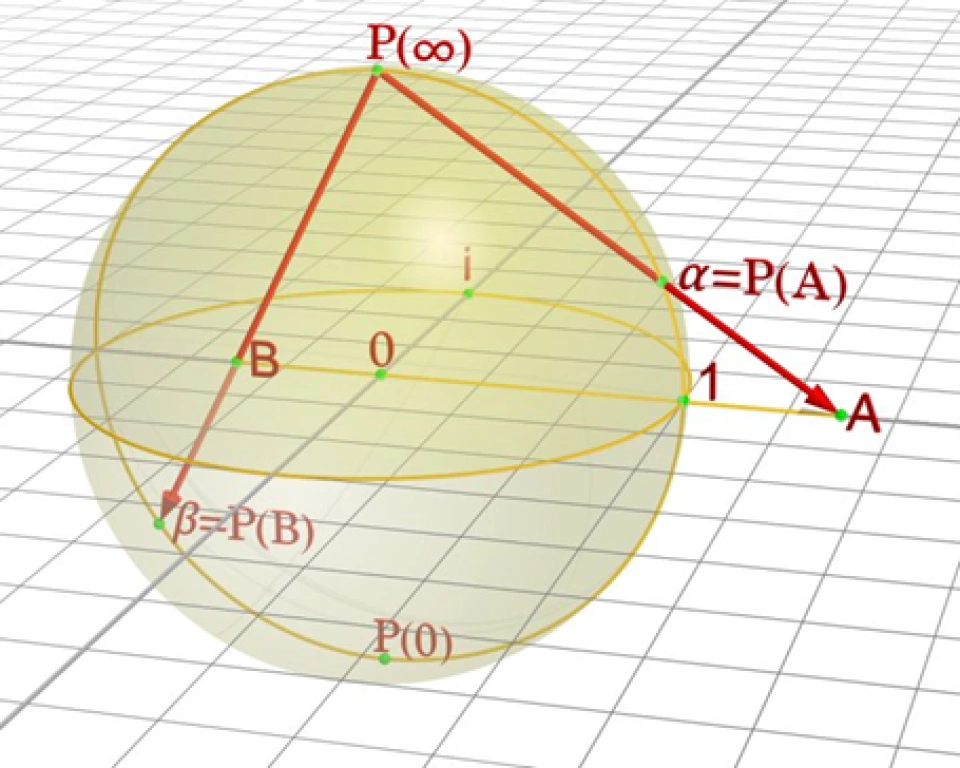
不过，通过类比的方法、通过二维球面，我们可以想象、刻画或理解三维球面的可能性质。在这里我们要介绍黎曼球面，它原本是黎曼(Riemann)在复分析中解释扩充复平面时引入的一种球极投影。现在我们利用这种思路在实空间中将球面从球的顶极点P向平面射影：
图源自维基百科
这就把球面上除了极点P之外的所有点映射到了一个无穷大的零亏格平面上，而且这个映射是双射且连续的（事实上其逆映射也连续）。接着黎曼定义平面上的无穷远处全部交于一点，该点称为无穷远点，作为球面的P点映射到平面上得到的结果。在这个意义下，0可以作为除数，并且满足：
注意，在其他任何意义下该式都不成立。
也就是说，二维平面∪{∞}同胚于
。
同样的，三维球面也可以做类似的投影，它可以描述为无洞的三维空间（也就是三维单连通流形）加上一个无穷远点。但是，我们知道三维球面向三维空间的映射是双射且连续的，并不知道其逆映射是否连续。也就是说，我们单知道三维球面可以被描述为三维单连通空间，不知道如果一个三维空间单连通，它是否一定能连续变化为三维球面。
这便是庞加莱猜想，他认为是这样的。
尾 声
前期做庞加莱猜想的大部分数学家，比如怀特海德(J.Whitehead)、哈肯(Haken)等人，他们给出的证明都是有缺陷的，但也为拓扑学的发展打下了坚实的基础。在这里我们只单独提一下赫里斯托斯·帕帕基里亚科普洛斯(Χρήστος Δημητρίου Παπακυριακόπουλος)，简称Papa。他把自己的一生都献给了庞加莱猜想，为此放弃了教授的职位。在他胃癌晚期撒手人寰的前夕，他还将自己证明庞加莱猜想的手稿交给他的朋友过目。然而仅仅翻了几页，他的朋友就发现了错误，但为了让Papa安心离去，朋友并没有告诉他。可以说，Papa的一生是一场悲剧，但对于他自己而言却是喜剧，因为他能够将自己的生命奉献给自己热爱的事业。
中期对庞加莱猜想作出巨大贡献的，主要是瑟斯顿
(Thurston)，他给出了几何化猜想，认为宇宙一定由八种基本拓扑形状构成，并利用几何化猜想证明了庞加莱猜想。然而，用猜想证明猜想当然是不严谨的，但瑟斯顿以跟希尔伯特(Hilbert)类似的理由
放弃了对几何化猜想的继续证明。他的理由是“要是证明出来了，年轻人就没有奋斗的动力了”。
最终，在克雷(Clay)数学研究所刚刚把庞加莱猜想加入“千禧年问题”后的不到三年，佩雷尔曼(Perelman)便完成了瑟斯顿“几何化猜想”的证明。2002年11月12日，佩雷尔曼在arXiv.org上公布了自己的证明，并在之后半年中又发布了两篇系列论文。这三篇文章概述了庞加莱猜想以及更一般的几何化猜想的证明，从而实现了哈密顿(Hamilton)提出的纲领。
到这里对庞加莱猜想的介绍就基本结束了，但我们还剩最后一个问题没有解决：为什么一个连数学符号语言都没有的、完全用自然语言描述的看似“显然”的猜想能困扰历代整整九十九年的数学家？
这个看似直观显然的猜想为什么如此难以证明，事实上是一般人难以理解的。所以在这里，我们不妨用问题来解释问题：如何证明一条闭合曲线把平面分为两部分呢？
这看起来可比庞加莱猜想显然多了，然而它的证明也是十分困难的，需要以基本群为工具才能给出证明。它的学名是Jordan曲线定理，直到1905年才出现第一个正确的证明。用自然语言叙述，它可能是一目了然的；但用数学语言叙述：
若J是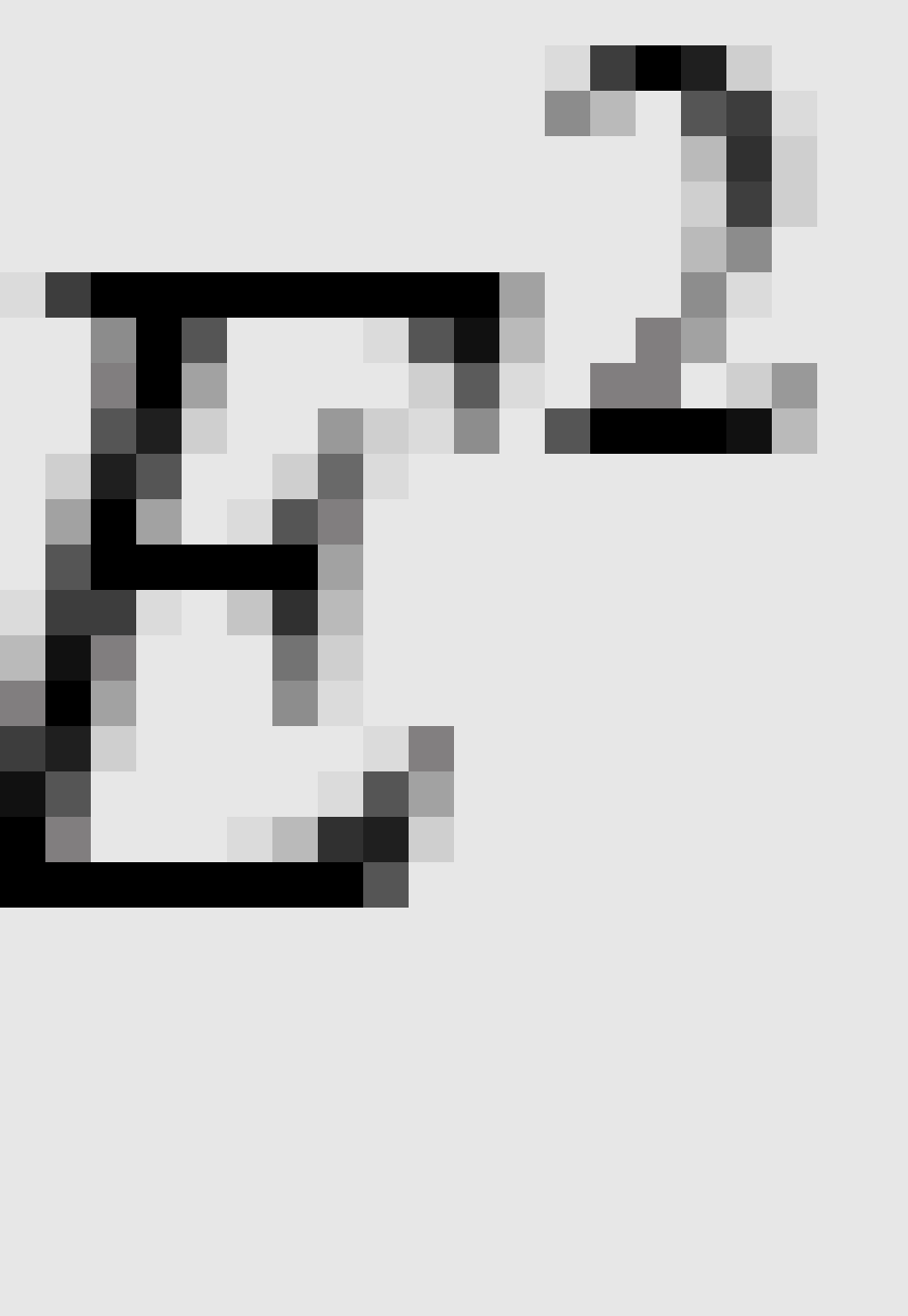
上的一条闭合Jordan曲线，则
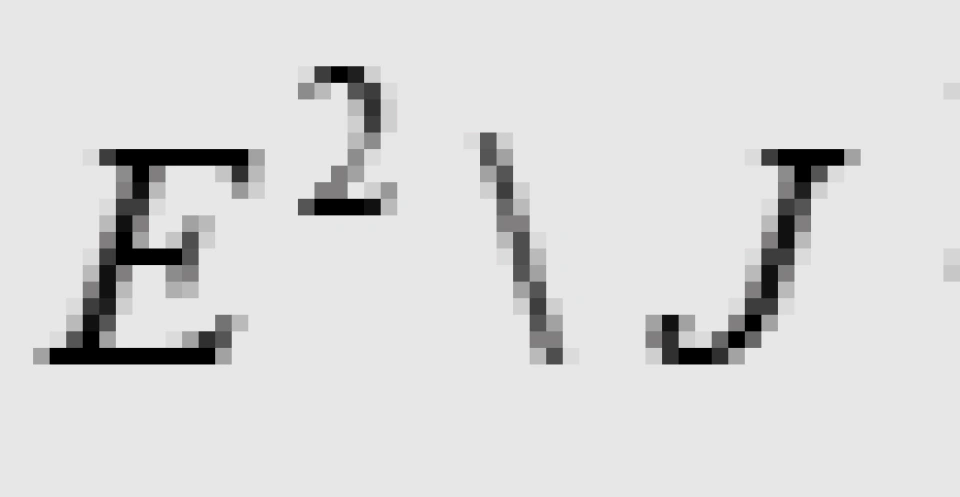有两个连通分支，它们都以J为边界。
看起来就没那么显然了。庞加莱猜想，也是类似的道理。所以，在科普的最后，我也要建议大家，不要认为表面显然的真实就是易懂的事实。不仅数学如此，人生，不也是一样的吗？
注 释
(1) 本文所使用的数学计算机辅助程序为Mathematica。该收缩过程可以用gif图展示，但是我的电脑在处理以下代码时失败了，有兴趣且电脑配置比较好的读者可以试着自己展示一下，代码见下：
F[u_, v_] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}
Animate[Show[
ParametricPlot3D[F[u, v], {u, 0, 2 Pi}, {v, 0, Pi},
PlotStyle -> Opacity[0.5]],
ParametricPlot3D[
a*F[u, v] /. {u -> t, v -> 1.5 + Sin[t]}, {t, 0, 2 Pi},
PlotStyle -> {Red, Thickness[0.01], Dashed}]], {a, 0, 1}]
(2) 这个秀儿一般的三维体是这样得到的：
ContourPlot3D[-1.` x^2*z^3 –
0.1125` y^2*z^3 + (-1.` + x^2 + 2.25` y^2 + z^2)^3 == 0.`,
{x, -1.5`, 1.5`}, {y, -1.5`, 1.5`}, {z, -1, 1.5`}]
(3) 除特别说明以外，本文讨论范围均在实空间内。
(4) 区别实际上是存在的，但是并不存在于1935年之前的大部分拓扑学家脑海中。一直到惠特尼(H.Whitney)提出了微分流形的严格概念之后，微分拓扑才真正开始兴起，拓扑学家才开始在原先同胚的基础上考虑“微分同胚”，即从连续过渡到光滑。比如，球体的表面显然是处处光滑的，但正方体却存在八个不光滑的奇点；所以这两个几何体虽然同胚但并不微分同胚。除特别说明以外，本文讨论范围均不包含微分性质。
(5) 四色定理的证明其实和庞加莱猜想还有一定的渊源。沃夫冈·哈肯(Wolfgang Haken)在证明庞加莱猜想的过程中发现了自己的一个致命错误，这次失败让Haken博士陷入了暴食症，后来被人戏称为“庞加莱猜想综合症”。最终在Haken转向研究“四色问题”后该病不治而愈了，而他最终也利用机器证明给出了四色定理的答卷（尽管并不是所有人都满意）。
(6) 圆环面的绘图：
r[u_, v_] := {1/2 (2 + Cos[u]) Cos[v], 1/2 (2 + Cos[u]) Sin[v],
Sin[u]/2}
ParametricPlot3D[r[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi}]
(7) 如下：
r[u_, v_] := {1/2 (2 + Cos[u]) Cos[v], 1/2 (2 + Cos[u]) Sin[v],
Sin[u]/2}
Show[ParametricPlot3D[r[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi},
PlotStyle -> Opacity[0.5]],
ParametricPlot3D[r[u, v] /. {u -> t, v -> t}, {t, 0, 2 Pi},
PlotStyle -> {Red, Thickness[0.01], Dashed}]]
(8) 图源自百度百科对“亏格”的介绍。
(9) 
(10) 斯梅尔(Smale)也在庞加莱猜想方面作出了一定的贡献，但他所做的工作并不是证明我们上文提到的常规的庞加莱猜想，而是证明了高维的、较简单的庞加莱猜想：
任何与n维球面同伦的n维封闭流形必定同胚于n维球面，其中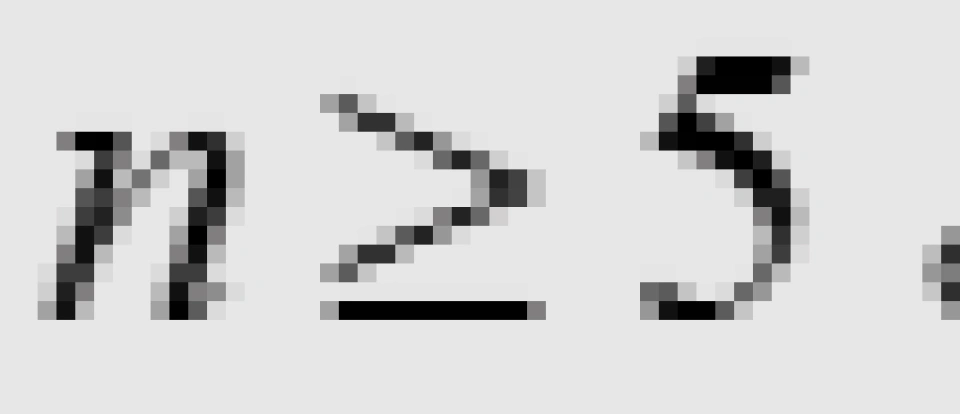
。
为什么高维的庞加莱猜想还要更简单？这就牵扯到纽结理论了。高维的情形下闭合曲线收缩的过程中不会打结，但三维中是会出现扭结的。
(11) 希尔伯特当年拒绝证明费马大定理(Fermat’s Last Theorem)的理由是：“这是一只会下金蛋的鹅，我为什么要杀掉它？”
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会将追究版权责任。】
更多科普资源和答疑，请加入耀星会科普官方QQ群：433646418
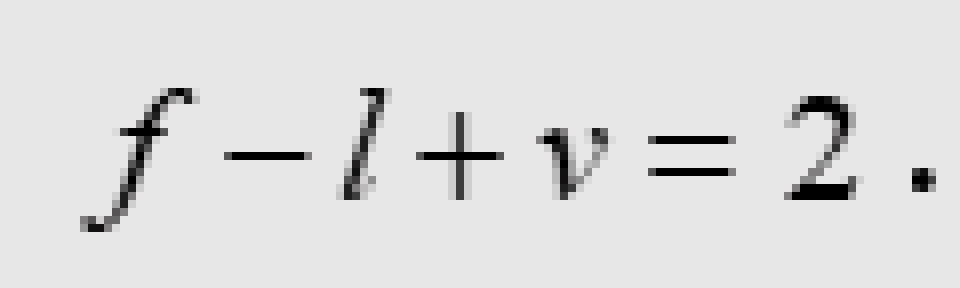
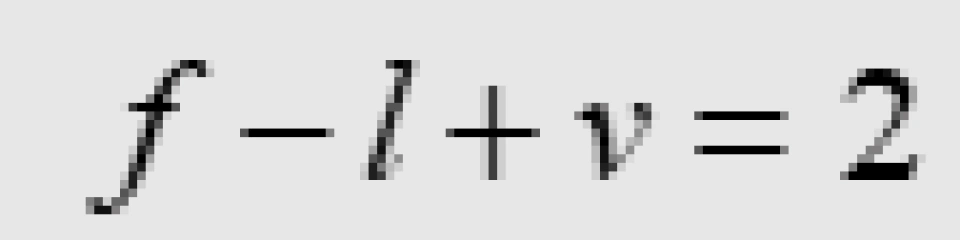
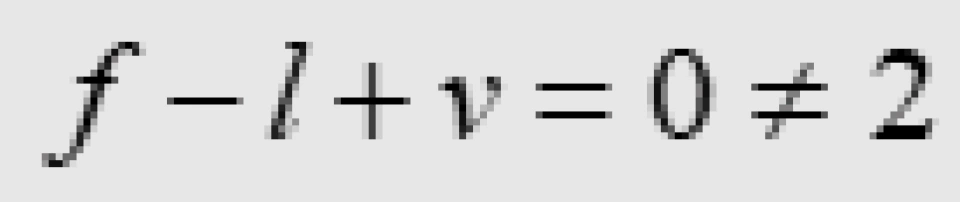
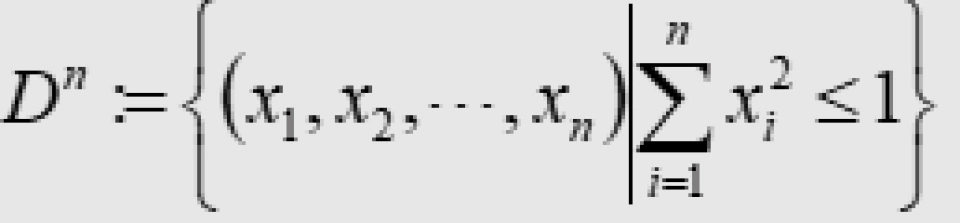
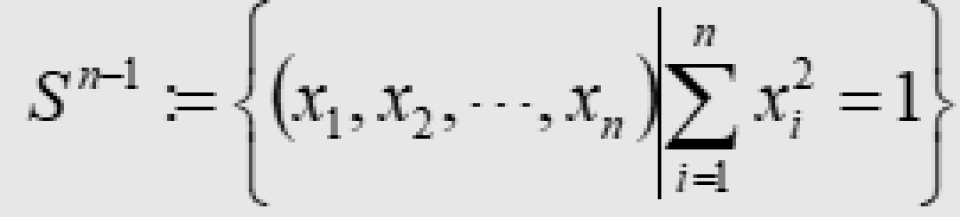
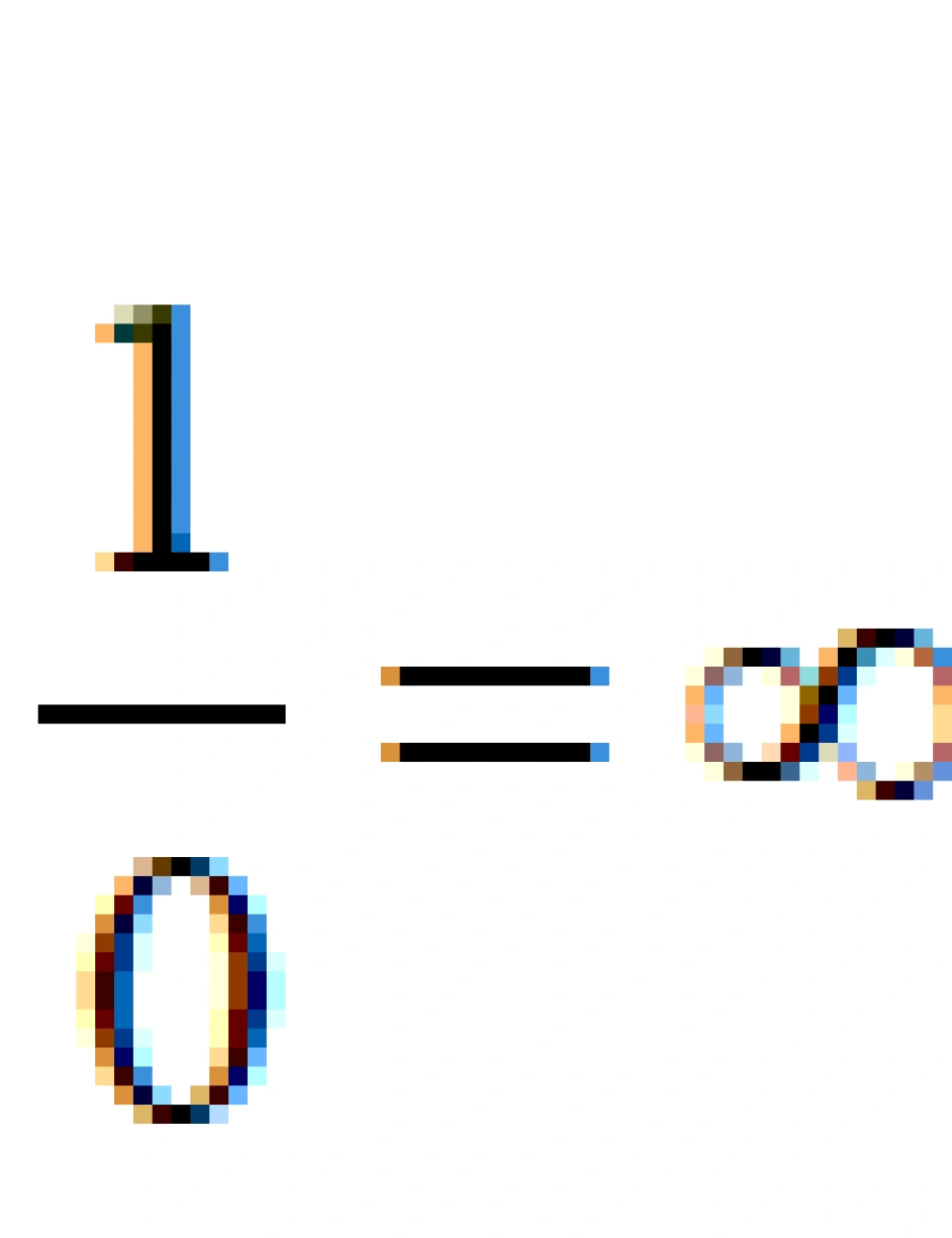
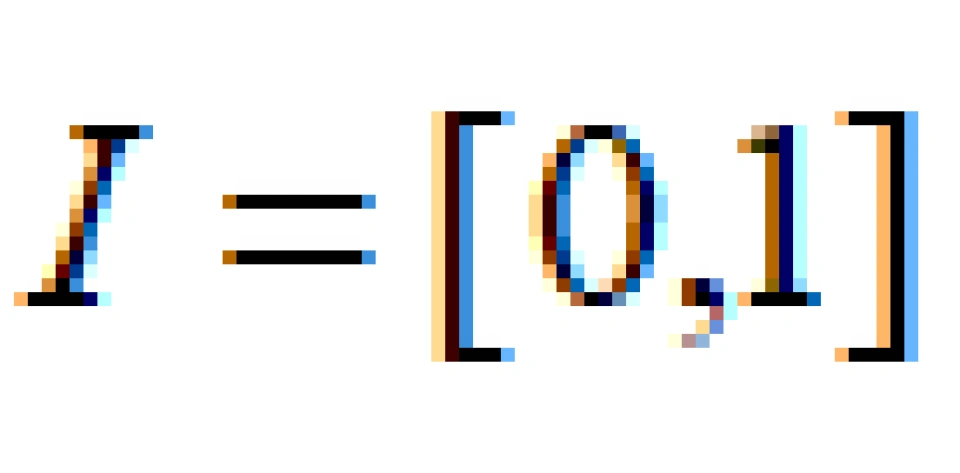
奖励金币：10
奖励理由：内容丰富饱满
这篇庞加莱猜想的文章够味，真不错。数学家们的脑洞也真大。
不过还是有点不理解，三维单连通空间为什么不能直接被捏成三维球形呢？
以及，为什么要强调边界，是不是因为维度的问题呢？
至于强调边界，我觉得更多是因为同伦与同胚的问题。